티스토리 뷰
MIT의 INTRODUCTION TO ALGORITHMS 수업을 바탕으로 공부하였고 정리합니다.
- 잘못된 내용이 있다면 댓글로 지적 부탁드립니다.
구구절절한 설명 시작
AVL tree는 Balanced Binary search tree라고 볼 수 있습니다. 기본 property가 BST이기 때문입니다.

중요한 점은 being balanced입니다. 이미 균형이 잡혀 있다는 것이 기본 속성이기 때문인데요. Balance factor의 부분이 AVL tree의 중요한 속성이기 때문에 이점을 중심적으로 보면 좋을 것 같습니다.
강의는 AVL trees의 definition, rotations, insert를 중점으로 봅니다.
Binary Search Tree(BSTs)의 경우, left/right subtree를 가집니다. 그리고 각 노드마다 key, left pointer, right pointer, parent pointer를 가집니다. 여기서 pointers를 가졌다는 점에서 heap과의 차이라고 볼 수 있습니다.
- heap은 tree로 시각화 가능한 일반 array
- BST는 pointer를 가진 tree
입니다.
그리고 이를 landing으로 비유했을 때, $k$ minutes 안에 다른 landing schedule이 없다면 set $R$에 $t$를 추가 할 수 있었습니다.
또한, left subtree의 모든 element는 root $x$보다 작으며, 반대로 right subtree의 모든 element는 root $x$보다 큼을 알 수 있습니다.
여기서 bst의 높이와 node의 높이의 차이를 설명합니다.
- root에서 leaf까지의 가장 킨 path를 h(height of BST)라 합니다. 즉, tree의 높이를 의미합니다.
- node의 길이는 각 node에서 leaf까지 내려가는 가장 긴 path입니다. 즉, root에서의 leaf의 node 길이가 곧 h이겠죠.
왼쪽 아래 그림을 보면 $h$의 최소~최대 길이가 $\theta (lgn)$에서 $\theta(n)$ 임을 알 수 있습니다.
balanced의 경우, log n의 길이이고 최악의 길이(하지만 bst는 성립하는 경우)는 n입니다.

그리고 노드의 높이는 'max(height(left child), height(right child)) + 1'로 계산할 수 있습니다. 왼쪽과 오른쪽 중 더 큰 높이에서 1을 더하면 됩니다.
오른쪽의 내용은 위에서 설명한 $lgn$과 $n$의 설명입니다.

AVL tree에서 가장 중요한 내용은 balance factor입니다. 이를 통해, 계속 balance를 유지하는 bst를 만들 수 있기 때문인데요.
이는 모든 노드의 left & right children의 높이 차이가 [-1,1] 이어야 한다는 뜻입니다. 쉽게 말하면 bf(balance factor)가 -1, 0, 1 이어야만 그 성질을 만족한다는 의미입니다.
bf는 $|h_l - h_r|$로 계산합니다. 왼쪽 node의 높이와 오른쪽 node의 높이 차의 절대값입니다. 이 절대값이 1보다 작거나 같으면 위의 속성을 만족합니다.
가장 최악의 경우는 오른쪽 subtre가 모든 노드에 대해서 왼쪽 보다 1씩 큰 경우라고 설명합니다. 이 의미는 아마 root 이외의 모든 값이 insert되는 모든 값이 더 큰 경우, 오른쪽으로 무한대로 내려가는 경우를 의미하는 것 같습니다. 그러면 높이가 n이고 n개의 노드를 갖게 됩니다.
따라서 가장 균형 잡힌(perfect balance) 경우는 n개의 노드를 가질 때 가능한 최대의 높이가 $lgn$일 때, 즉 노드의 개수가 $2^h$일 때 입니다.
높이를 h라고 고정했을 때 넣을 수 있는 최소 노드의 개수가 $2^h$개가 됩니다. 이 부분이 수학 바보라서 이해가 잘 안 갔는데 위에는 제가 좀 잘못 필기한 것 같습니다. 아래 설명 참고!

해당 경우에, tree의 높이 h는 3이 되죠. root에서 가장 아래의 leaf까지 세 번 내려가기 때문입니다.
그리고 여기서 n이 의미하는 걸 필기엔 개수라 적어놨는데 edges의 개수 같습니다. 그래서 root가 가지는 edge의 개수는 8이 되고, log8(height of node)=3(height)이므로 이렇게 계산이 된다고 이해했습니다.
*잘못 이해했다면 말씀해주세요😭

이제 insert를 설명하기 위해 balance factor를 통해서 BST를 구성해주는 부분입니다. 그리고 BST를 만들기 위해 node를 위로 change 해주는 과정이 추가 됩니다.
$x$가 AVL property를 위반하는 가장 낮은 노드이고, $x$가 right쪽으로 더 깁니다. 해당 경우를 right heavy라고 합니다.
따라서 왼으로 회전 시켜줍니다. 오른쪽이 무거우니까 왼쪽으로 옮긴다고 이해하면 빠를 것 같습니다.
- x를 left rotate한다 → left rotate(x) / LR(x)
그럼 x가 왼쪽으로 내려가고, y가 위로 올라옵니다. 그리고 y의 child node이던 B의 경우, y보다 작으니 left subtre(x)로 내려가고, x < B이므로 x의 right child로 자리 잡습니다.
그리고 bf를 고쳐줍니다. 그럼 모두 차이가 2 이상 나지 않게 되며 AVL이 완성됩니다.
else의 경우, right heavy에 속하며 두 번 rotation해야 해서 double rotation에 해당됩니다. 이 경우엔 root의 이동이가장 마지막에 이루어집니다. subtree에서 먼저 위반하는 애를 rotate 시켜 줍니다.
따라서
- right-rotate(z) - z를 오른쪽으로 회전시켜서 y가 z의 parent node가 됩니다. (그림에선 한 단계 생략됨) y의 child node로 B와 z가 오게 되고, z의 child node로 C와 D가 오게 됩니다.
- left-rotate(x) - root에 있는 x를 왼쪽으로 회전 시켜서 y가 root가 되도록 합니다. 그럼 y의 child node로 left는 x, right는 z가 자리 잡게 되며, y의 left child였던 B가 자연스럽게 x의 right child까지 내려갑니다.
정리하자면,
AVL sort는 n개의 item을 insert합니다. in-order traversal로 호출하면 $\theta(n)$이 걸리며 linear time이 소요됩니다.
구체적인 예시

n개의 항목을 삽입할 때, 각 h만큼 걸리는데 h가 $O(lgn)$만큼 걸린다는 것이 보장됩니다.
rotation의 경우, 교환하는 것이기 때문에 $O(1)$ time이며, 나머지 insert, search, delete 모두 $O(lgn)$에 해당됩니다.
마지막 정리 내용

4 cases (single rotation, double rotation) ‼‼‼
이 네 가지 경우를 이해한다면, AVL tree를 전부 이해했다고 보면 될 것 같습니다.
- Left Left
- Left Right
- Right Right
- Right Left
- 1번과 3번의 경우는, 왼쪽과 오른쪽으로 heavy하게 떨어지는 경우입니다. 따라서 각 반대쪽으로 회전을 시켜주면 균형잡힌 트리가 완성됩니다. AVL 코드를 참고하면 더 좋을 것 같은데, rotation 하는 함수에서 기존의 child도 비교를 통해 이동하게 됩니다.
- 2번과 4번의 경우는 지그재그 형태입니다. 따라서 1, 3처럼 heavy한 형태로 먼저 바꿔준 다음에 다시 rotation을 수행시켜줘야 합니다.
정리!
1. Left Left - single rotation / Right rotate(z): balance factor를 2로 갖는 root를 rotation 시켜줍니다.
2. Left Right - Double rotation / Left rotate(y) → Right rotate(z) : balance factor를 기준으로 2가 되는 root를 rotation 시켜주면 됩니다.
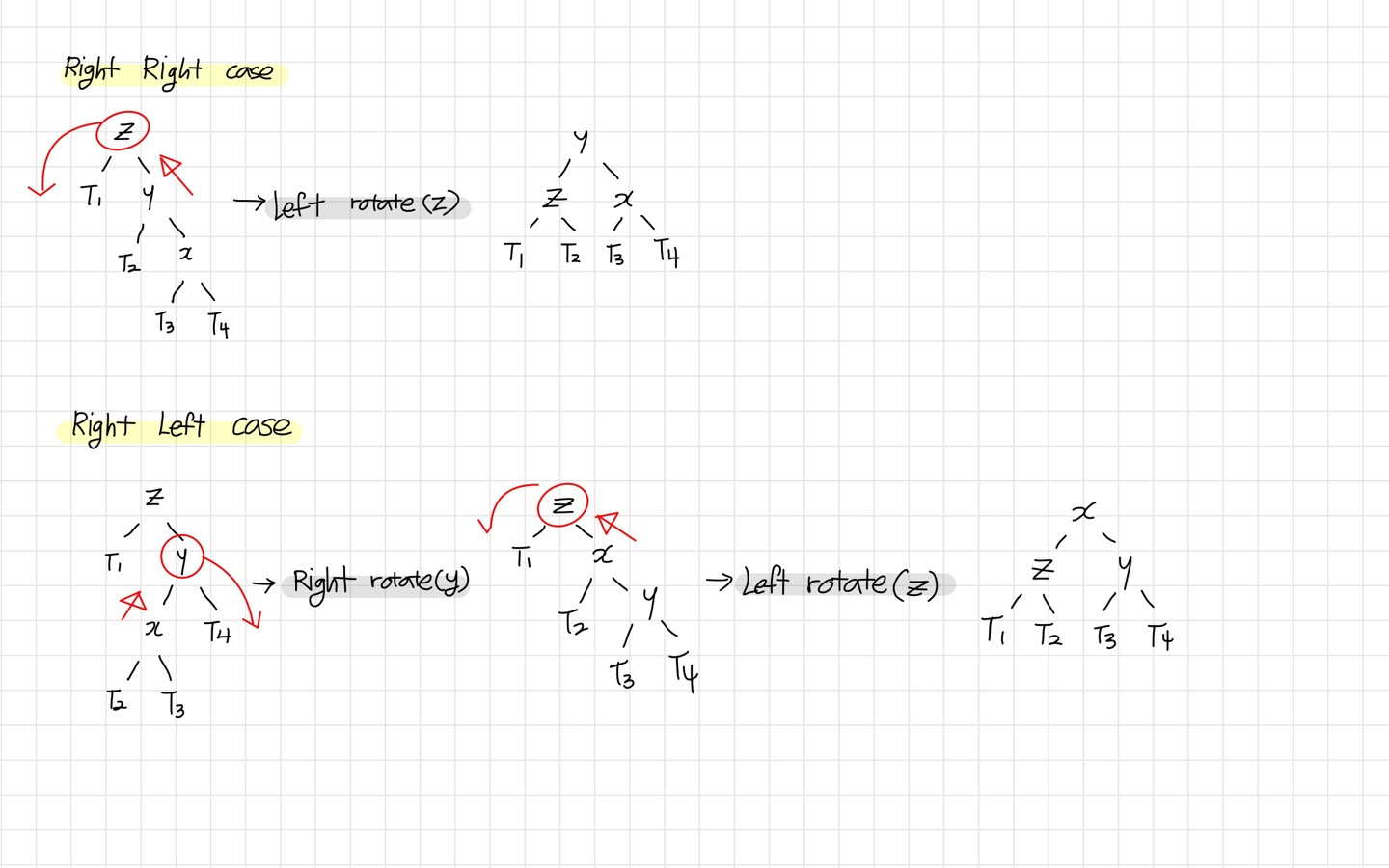
3. Right Right - single rotation / Left rotate(z): 설명 위와 동일
4. Right Left - Double rotation / Right rotate(y) → Left rotate(z): 설명 위와 동일

'Skills > DS & Algorithms' 카테고리의 다른 글
| Peak Finding in 1 or 2D array (0) | 2022.10.24 |
|---|---|
| [Sorting] Insertion, Merge Sort (2) | 2022.09.21 |
| 자료구조 면접 대비 간단 요약 정리 (0) | 2022.08.02 |
- Total
- Today
- Yesterday
- 파이썬
- cs231n
- Unsupervised learning
- clip
- 서버구글드라이브연동
- prompt learning
- CNN
- 도커 작업
- 퓨샷러닝
- 도커 컨테이너
- 리눅스 nano
- 도커
- 리눅스
- 파이썬 클래스 다형성
- 프롬프트
- few-shot learning
- 구글드라이브연동
- 딥러닝
- 리눅스 나노
- 리눅스 나노 사용
- Prompt
- style transfer
- support set
- python
- NLP
- stylegan
- 파이썬 딕셔너리
- linux nano
- docker
- 파이썬 클래스 계층 구조
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

