티스토리 뷰
MIT의 알고리즘 수업 강의 자료를 참고하였습니다.
왜 정렬하는가?
- 확실한 응용 사례
- MP3 보관함 정렬
- 전화번호부 정리
- 검색하기 쉬움
- 정렬하면 쉬워지는 문제들
- 중간값 또는 가장 가까운 쌍 찾기
- 이진 탐색, 통계적 이상치 확인
- 응용 사례
- 데이터 압축
- 컴퓨터 그래픽(화면 렌더링)
Finding a median
중간값을 찾아보겠습니다. 정렬되지 않은 배열 A를 정렬된 B로 바꾸려고 합니다.
array A[0:n] → B[0:n]
unsorted → B[n/2]
- 입력값으로 비교 함수를 갖는 정렬 알고리즘이 있다면 충분한 시간이 흐른 뒤에 정렬된 배열 B를 얻을 수 있음
- 정렬된 배열이 있다면 상수의 시간이 걸림
Binary Search
이진 탐색을 하는 경우입니다.
A[0:n] looking for specific item $K$
compared k → B[n/2]
- k를 B[n/2]와 비교합니다.
- B는 정렬되었고 배열의 절반만 보게 됩니다.
Insertion Sort
삽입 정렬입니다. 배열의 모든 요소를 배열의 시작부터 끝까지 비교해 가면서 적절한 위치에 삽입하는 정렬 알고리즘입니다.
For $i = 1, 2, …, n$
insert $A[i]$ into sorted array $A[0:i-1]$
by pairwise swaps down to the correct position
예시를 살펴보겠습니다. 아래 [5, 2, 4, 6, 1, 3]의 배열이 있다고 가정합니다.
5 2 4 6 1 3
2 → key
5와 2를 비교하고, 2가 더 작으니까 key로 지정합니다.
swap (1) - 2와 5를 바꿉니다.
2 5 4 6 1 3
4 → key
5와 4를 비교하고 4를 key로 지정합니다.
swap (2) - 4와 5를 바꿉니다.
해당 과정을 반복합니다.
2 4 5 6 1 3
6 → key

swap (3)
1 2 4 5 6 3
3 → key

swap (4)
1 2 3 4 5 6

Q. How many steps do I have?
A. $\theta(n)$ steps (key positions)
몇 번의 스텝이 있었습니까? $\theta(n)$ 의 steps이 존재하게 됩니다.
그 의미는 키의 이동도 포함해서 각 단계에서 $\theta(n)$ 만큼 수행하고, 여기서 swap은 $\theta(n)$ 번 compare과 swap을 한다는 걸 의미합니다.
- each step is $\theta(n)$ swaps.
- 각 단계가 $\theta(n)$ 이기 때문에 $\theta(n^2)$ algorithms이다.
- $\theta(n^2)$ compare & $\theta(n^2)$ swaps
Compare >> swaps
- 실제론 비교가 대체적으로 더 높은 비용이 듦
- 하지만 같다고 가정하고 살펴볼 것
- $\theta(n^2)$ comparrison set
compare with the middle → Binary search
I’m going replace this(pairwise swaps) with binary search. Do a binary serach on $A[0:i-1]$ already sorted in $\theta(n log n)$ time.
- pariwise swaps을 Binary Search로 바꾼다.
- 이미 정렬되어 있기 때문에 Binary search는 $\theta(log n)$ 시간이 걸림
- 하지만 삽입 후 항목을 옴기는 것도 $\theta(n)$ 시간이 걸리므로
- $\theta(n log n)$만 비교하면 된다.
- $\theta(n^2)$ swap → $\theta(n log n)$
merge sort로 넘어가기 전에 해당 개념을 살펴보겠습니다.
Divide and Conquer
분할 정복은 문제를 분할하고, 분할한 문제를 해결한 다음에 결과를 조합하는 알고리즘입니다. 큰 문제를 작은 문제로 분할한다는 관점에서 하향식 접근 방법(Top-down)으로 문제를 푼다고 볼 수 있습니다.
- 분할: 문제를 동일한 유형의 여러 하위 문제로 나누는 것
- 해결: 가장 작은 단위의 하위 문제를 해결하는 것
- 조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합하는 것
분할 정복 알고리즘은 보통 재귀를 사용하여 구현합니다.
아래의 코드는 분할 정복의 대표적인 문제인 피보나치 수열 코드입니다.
def fibb(n):
if n <= 1:
return 1
return fibb(n-1) + fibb(n-2)
Merge sort
합병 정렬도 Divide&Conquer(분할 정복)을 사용합니다.
A[0:n]
L= A[0:n/2-1] R …

[ A ]
Split two parts → L and R
- Left와 Right로 나눕니다.
Sort
L’ R’
- 정렬합니다.
Merge
- 정렬된 L'과 R'을 합칩니다.
sotrted array A
- input size: $n$
- two arrays of size $n/2$
- 2 sorted arrays of size $n/2$
- sorted array of size $n$
→ 입력값의 크기는 n이고, 정렬되어 있는 두 개의 n/2의 크기의 배열을 갖습니다. 결국 n의 크기를 갖는 정렬된 배열을 갖게 됩니다.
merge algorithm이 작동하는 예시를 살펴보겠습니다.
- Merge: Two sorted arrays an input
| L' | R' |
| 20 | 12 |
| 13 | 11 |
| 7 | 9 |
| 2 | 1 |
→ 1 2 7 9 11 12 13 20
정렬된 값을 얻을 수 있습니다.

해당 과정은 기본적으로 차례차례 올라갑니다. 몇 개의 포인터가 있고, 두 개의 배열을 비교하며 올라갑니다. 이게 바로 merge routine입니다.
모든 과정 중 실제 작업은 merge routine에서만 일어납니다. 정렬의 나머지 과정은 단순한 재귀 호출이기 때문인데요. 배열을 쪼갤 필요가 있습니다.
그 방법은 간단합니다.
배열 A[0:n]이 있다고 하면, n이 홀수인지 짝수인지에 따라 L을 A[0:n/2-1]라고 정하고 R도 비슷하게 나눕니다.
이 부분에서 코드를 짤 때 고민을 좀 했었는데, 홀수라면 2로 나누었을 때 정수로 떨어지지 않으니까 정수로 만들어줄 필요가 있었습니다. 그때 round 함수가 떠오르긴 했지만, 반올림을 하는게 반으로 나누는데 적절한 것 같진 않았습니다.
보통 인덱스가 0부터 시작하니까 우리는 실제로 n까지의 배열을 갖는다면 그 총 개수는 n보다 1이 더 많다고 생각이 들어서 전 math module의 ceil(올림) method를 사용하였습니다.
다시 수업 내용으로 돌아가서,
Q: 크기가 n/2인 두 배열이 있다면 합병 정렬의 복잡도는 얼마일까요?
A: $\theta(n)$입니다.
하지만 해당 알고리즘의 전체 복잡도는 $\theta(n log n)$입니다. 이것을 증명하기 위해 merge sorting 전체를 살펴봅니다. 그러기 위해 recursion tree를 살펴보게 됩니다. 이는 그림으로 증명하는 방법입니다.
Complexity

$T(n) = c_1 + 2T(n/2) + c n$
$= \alpha T(n/2) + \theta(n) + \theta(1)$
- c1(divide): 배열을 나누기 위해 필요한 상수 시간
- 2T(n/2): 크기가 n/2인 두 가지 문제, 재귀 부분
- cn: merge 부분으로 상수 곱하기 n인데 이것은 $\theta(n)$의 복잡도와 관련된 것입니다.
트리 구조로 복잡도를 계산해보면 식이 아래처럼 나열됩니다.
c n
cn/2 cn/2
cn/4 cn/4 cn/4 cn/4
c - constant
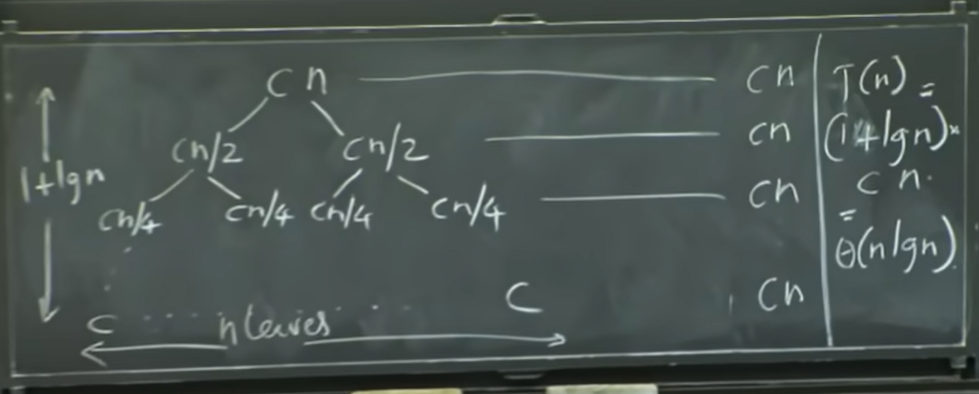
해당 과정을 거치면 log(n)+1과 n개의 단말 노드가 생깁니다.
이 트리를 더 살펴보면 각 단계에서 작업을 진행하는데, 각 레벨마다 cn만큼의 작업을 진행합니다.
cn으로 모두 같습니다. 같은 양의 작업을 하는 것입니다.
이제 이 모든 작업이 (1+log(n)) 만큼 임을 알 수 있고, $(1+log(n)) \times cn =$ $\theta(n log n)$ 임을 알 수 있습니다.

$T(n) = (1 + logn) \times cn = \theta(nlogn)$
$T(n) = c_1 + 2T(n/2) + c n$
$= 2 T(n/2) + \theta(n) + \theta(1)$
What is one advantage of insertion sort over merge sort?
- You don’t have to mote elements outside.
- In-place sorting is something that has to do with auxiliary space
- 삽입 정렬은 요소들을 정렬하기 위해 추가적인 공간이 필요 없습니다. 제자리 정렬이기 때문인데요.
- 합병 정렬은 $L^\prime, R^\prime$이 필요합니다. 초기 정렬인 L과 R과는 다릅니다.
Merge - sort $\theta(n)$ auxiliary space (추가 공간이 필요함)
In-place sort → $\theta(1)$ auxiliary space (일정한 보조 공간을 가집니다.)
- In-place merge-sort: 제자리 합병 정렬이란 것이 있음(참고만)
- Merge sort in Python: $2.2 n log n$ ms
- Insertion sort in Python: $0.2 n^2$ ms
- Insertion sort in C: $0.01n^2$ ms
Recurrence solving




해당 강의에서 중요한 내용은
- 병합 정렬 방법 작동 원리
- Time complexity: Recursion Tree
- Space complexity: auxiliary space
- Recursion 있을 때, $T(n)$을 구하는 여러 cases
입니다.
감사합니다.
[Reference]
'Skills > DS & Algorithms' 카테고리의 다른 글
| Peak Finding in 1 or 2D array (0) | 2022.10.24 |
|---|---|
| [Tree] AVL Tree (Balanced BST) - 균형 이진 탐색 트리 (0) | 2022.10.12 |
| 자료구조 면접 대비 간단 요약 정리 (0) | 2022.08.02 |
- Total
- Today
- Yesterday
- 프롬프트
- 퓨샷러닝
- few-shot learning
- 도커 작업
- 리눅스 nano
- 구글드라이브연동
- support set
- 도커
- 파이썬 딕셔너리
- cs231n
- Prompt
- 파이썬 클래스 다형성
- Unsupervised learning
- CNN
- 서버구글드라이브연동
- 딥러닝
- clip
- 도커 컨테이너
- 리눅스 나노 사용
- python
- NLP
- 파이썬 클래스 계층 구조
- 파이썬
- stylegan
- 리눅스 나노
- 리눅스
- prompt learning
- docker
- style transfer
- linux nano
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

