티스토리 뷰
Peak Finder
peak을 찾는 것이 주제입니다!
- Find a peak if it exists
- a peak: 극대값이 여러 개여도 하나만 찾으면 됨
- if it exists: 극대값의 정의에 따라 배열에 극대값이 존재 여뷰가 갈림. 따라서 이 조건이 붙음
두 가지 버전이 있는데, 1-dim과 2-dim입니다.
One-dimensional Version
여기서는 Position 2와 9가 peak이라고 합니다. 대신 조건으로 $b \ge a$, $b \ge c$이고, $i \ge h$이어야 합니다.

앞에서부터 직진하면서 시작하고, left에서 시작하게 될 경우, 평균적으로 n/2개를 살펴보게 될 것입니다. 그리고 가장 worst case는 모든 n개를 다 살펴보는 경우가 됩니다.
Complexity는 어떨까요?
peak가 array의 i 번째에 있다면 i개의 원소를 검사해야합니다. 따라서 최악의 시간 복잡도 는 peak가 n 번째에 있을 때 이므로 $T(n) = O(n)$ 이 되고, 선형 시간 알고리즘입니다. → $$
이것보단 좀 더 효율적인 방법이 있습니다.

그렇다면 중간에서 시작하는 건 어떨까요? 시작부터 n/2 지점에서 보는 겁니다.

그러면 이제 중간을 기준으로 어느 쪽이 더 큰 값이 있는지 방향을 어떻게 고를 것이고 n/2개 이상의 element를 살펴보는 경우도 있을 겁니다.
그래서 선택한 방법은 n/2 position부터 보되, a[n/2]에서 a[n/2 -1]과 a[n/2 +1]을 비교하는 겁니다.
- if a[n/2] $\nless$ a[n/2 -1], 이땐 1부터 n/2까지 왼쪽 절반에서 peak을 살펴봅니다.
- else a[n/2] $\nless$ a[n/2 +1], 이땐 n/2부터 n까지 오른쪽 절반에서 peak을 살펴봅니다.
- else n/2 position이 peak일 수도 있습니다.
- 따라서 a[n/2] $\ge$ a[n/2 − 1], a[n/2] $\ge$ a[n/2 + 1]로 설정합니다.

Complexity는 어떨까요?
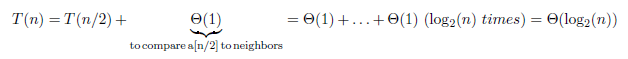
위와 같이 $\theta(i)$를 합하려면, 모든 경우에 적용되는 상수를 찾아야 합니다. $\theta(1)$은 peak인지 확인하는 부분이고, 양 옆과 비교를 하면 총 3번 확인하게 되고, 모두 $\theta(1)$이고, 따라서 중간 원소가 peak가 아니라면 n/2을 다시 검사해야하기 때문에 최종적으로 $T(n)=O(1)+O(1)+O(1)+O(1)+...+O(1)=O(logn)$이 됩니다.
단순히 $O(n)$의 선형 알고리즘일 때 보다 log일 경우, 훨씬 더 효율적입니다.
n = 1000000 인 경우, 파이썬에서 $\theta(n)$ 알고리즘을 실행하는데 13초가 걸립니다. $\theta(logn)$ 알고리즘은 0.001초 밖에 걸리지 않습니다.
Two-dimensional Version

a가 $a \ge b, a \ge d, a \ge c, a \ge e$인 경우 2D-peak 입니다.

여기선 동그라미친 20이 peak입니다.
Attempt 1 : Extend 1D Divide and Conquer to 2D

- 먼저 column의 중간값을 찾습니다. → $j=m/2$
- $i, j$에서 1D-peak을 찾습니다.
- $(i, j)$를 시작 지점으로 해서 i행에서 1D peak을 찾습니다.
Attempt 1 - Fail
해당 시도는 실패할 수 있습니다. 그 이유는 2차원 극댓값이 i행에 존재하지 않을 수 있기 때문입니다.

단순히 14를 2D-peak으로 고르고 끝이 날 수 있습니다.
Attempt 2
- 먼저 column의 중간값을 찾습니다. → $j=m/2$
- $j$열에서 가장 큰 $(i, j)$ 값을 찾습니다.
- 그리고 $(i, j-1)$, $(i, j)$, $(i, j+1)$을 비교합니다. 즉, 같은 행에서 양 옆의 column들, 좌우 값과 비교합니다.
- $(i, j-1)$ < $(i, j)$라면 왼쪽 열을 고릅니다.
- 오른쪽일 경우도 동일합니다.
- 위 두 condition을 만족하지 않으면 $(i, j)$가 2D-peak이다.
- 그렇다면 column의 절반으로 줄어든 새로운 문제를 푼다.
- column이 1개 남았을 때, 최댓값을 찾고 끝납니다.

아래의 경우에 해당합니다.
1번째 column을 뽑았고(index가 0부터라고 했을 때, index 1인 column), 거기서 최댓값은 (3,1)인 17이 max값입니다. 그리고 양옆을 비교합니다. 오른쪽에 존재하는 19가 더 큽니다. 그러면 이제 절반으로 줄어든 2개의 column을 통해 또 시도합니다. 19보다 20이 더 크고, 20이 있는 마지막 1개의 column에서의 최댓값은 21이 됩니다.
Complexity는 어떨까요?
n개의 행과 m개의 열이 있는 문제였고, 이를 T(n,m)이라고 하면

m개의 column을 절반으로 나누고, 거기서 maximum을 찾는데 n개의 row이기 때문에 $\theta(n)$이 걸립니다. 만약에 column이 1개라면 시간 복잡도는 $T(n,1)=\theta(n)$이 걸리게 됩니다.
즉, T(n,m)은 row 수만큼 반복해서 n이 곱해지게 되며, $\theta(n)$이 $logm$개 있게 되어 $\theta(nlogm)$이 됩니다. (O(rows * log(columns)))
여기서 설명한 Attempt 1과 2는 각각 Greedy 알고리즘과 분할 정복 알고리즘에 해당한다고 합니다. 첫 번째 탐욕 알고리즘 같은 경우는 시작 원소를 정한 다음, peak가 아니라면 주변 원소 중 더 큰 원소를 선택하며 계속 비교를 통해 peak인지를 확인하는 경우였습니다. 두 번째는 Divide & Conquer이 1차원을 확장하여 column을 절반만 보게 된다는 특징이 있습니다.
'Skills > DS & Algorithms' 카테고리의 다른 글
| [Tree] AVL Tree (Balanced BST) - 균형 이진 탐색 트리 (0) | 2022.10.12 |
|---|---|
| [Sorting] Insertion, Merge Sort (2) | 2022.09.21 |
| 자료구조 면접 대비 간단 요약 정리 (0) | 2022.08.02 |
- Total
- Today
- Yesterday
- docker
- cs231n
- CNN
- 리눅스 nano
- 도커 작업
- 리눅스 나노
- stylegan
- style transfer
- NLP
- support set
- prompt learning
- 리눅스
- 프롬프트
- 파이썬 클래스 계층 구조
- linux nano
- python
- Unsupervised learning
- Prompt
- 파이썬 딕셔너리
- 리눅스 나노 사용
- 딥러닝
- 서버구글드라이브연동
- 파이썬 클래스 다형성
- clip
- 구글드라이브연동
- few-shot learning
- 퓨샷러닝
- 파이썬
- 도커 컨테이너
- 도커
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

