자료 출처: CS5670 Lec 11
이번 11강은 Panorama에 대한 내용입니다. 저번 강의에서 반복되었던 Projection matrix 개념의 연장선이기도 합니다.
Intro

각 이미지를 warping 시키는 방법은 무엇이 있었나요? Homography를 계산하여 수행할 수 있었습니다.
그렇다면 360도 파노라마를 만들기 위해 homography를 사용할 수 있나요? 정답을 먼저 말하면 이 방법으론 360 panorama를 만들 수 없습니다. 대신 이 질문에 대한 아이디어는 이미지를 평면으로 투영하는 것이 될 수 있습니다.

Image mosaic
모자이크란 3D로 자연스럽게 해석될 수 있는데 이미지가 공통 평면에 재투영 된다는 점에서 오른쪽의 평면에 모자이크가 형성됨을 알 수 있습니다.
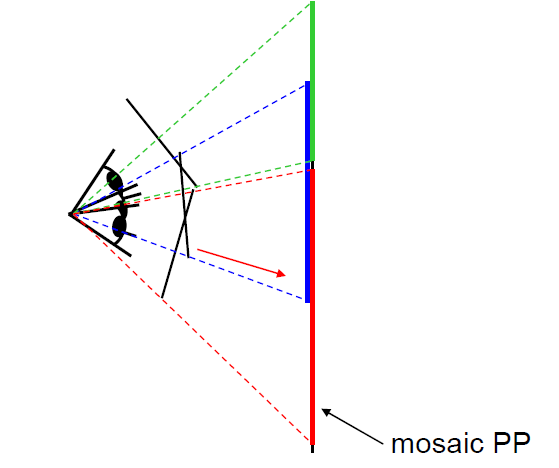
모자이크란? 여러 장면(scene)에 대한 이미지들을 촬영한 후, 이들을 결합하여 모든 방향을 바라볼 수 있도록 합성된 영상을 의미합니다. 하나의 scene에 대한 넓은 시야(FOV: Filed Of View)를 가집니다. 여러 장의 이미지를 연결해서 seamless한 결과물을 갖는 것이 목표입니다. 즉, 여러 장의 이미지를 부드럽게 연결하고자 합니다.
Geometry interpolation of mosaics
아까 위의 질문을 다시 떠올려 봅시다.
만약 모든 360도의 선을 캡처한다면, 360도 파노라마를 만들 수 있습니다. 가장 기본적인 operation은 한 평면에서 다른 평면으로 이미지를 투영하는 것입니다.
projective transformation(Homography)는 scene이 독립적이다고 할 수 있습니다.

How to create a mosaic
- 같은 위치에 있지만 카메라 각도가 다른 여러 개의 동일한 scene image가 있다고 가정합니다.
- 두 이미지 평면 간의 매핑은 scene의 깊이와 무관하게 homography임을 보여줍니다.
- 왼쪽 이미지에서 점들을 찾고, 이미지 특징을 기반으로 오른쪽 이미지에서 대응하는 점을 찾을 수 있습니다.
- homography는 8 자유도를 가지므로 4개의 대응하는 쌍으로 문제를 제안할 수 있습니다.
- 같은 위치에서 다른 방향으로 촬영한 여러 이미지를 스티칭하여 angle image를 구축합니다.
여기서 위에서 설명했던 scene-INDEPENDENT한 특성을 설명할 수 있는데, depth와 같은 scene structure와 무관하게 카메라의 내부 파라미터와 포즈에만 의존하기 때문이라 볼 수 있습니다
Creating a panorama
Basic Procedure
- 같은 위치에서 일련의 이미지를 가져옴 (optical center에서 카메라를 회전)
- 첫 번째와 두 번째 이미지 사이의 transformation을 계산
- 첫 번째 이미지에 두 번째 이미지가 overlap 되도록 transform
- 두 이미지를 blend하여 mosaic를 만듦
- 이미지가 더 있다면, 반복
결국은 일련의 사진을 찍어 연결하는 과정입니다.
해당 강의에서는 transformation을 계산하는 방법으로 calibration을 통해 다시 한 번 더 설명합니다.
Image reprojection

같은 카메라 센터에서 나온 두 이미지를 어떻게 연결시킬 수 있을까요?
PP1의 각 픽셀을 통해 ray를 투사시키고, 해당 ray가 PP2와 교차하는 픽셀을 그립니다.
What is the transformation?
이미지 2에 있는 point를 어떻게 이미지 1로 mapping 할 수 있나요?

여러 이미지를 panorama 영상으로 합치기 위해 모든 이미지를 하나의 같은 평면으로 투영시켜야 합니다. 이것이 가능하기 위해 영상들이 Homography 관계에 있어야 합니다. camera matrix P를 생각하며 step 1, 2, 3의 과정을 계산해보겠습니다.

- step1에서 이미지 2의 픽셀을 카메라 2 좌표계의 ray로 변환해야 합니다. 따라서 이미지 2의 intrinsic parameter인 $K_2$의 역변환을 곱하는 형태를 가집니다.
- step2에서 카메라 2 좌표계의 ray를 카메라 1 좌표계 ray로 변환해야 하므로 이미지 2의 extrinsic parameter인 $R_2$의 transpose를 굽한 형태를 가집니다.
- step3에서 카메라 1 좌표계의 ray를 이미지 1 좌표계의 픽셀로 변환해야 합니다. 이미지 1의 intrinsic parameter인 $k_1$을 곱한 형태로 가집니다.
추가 정보
- $K$는 Camera Calibration Matrix로서 카메라 좌표계 상에서 3D point와 그것이 투영되어 얻어진 이미지 면에서의 2D point와의 관계입니다.
- 행렬 K에 포함되어 있는 parameter들을 카메라의 internal parameter라 불렸고, focal length, aspect ratio, skew principal point를 나타냅니다.
- R과 t는 카메라의 Rotation Matrix와 Translation Vector로서 월드 좌표계와 카메라 좌표계의 변환 관계를 나타냅니다.
- 이는 카메라의 projection center를 고정시키고 카메라를 일정량만큼 회전 시킨 후에 얻은 이미지를 회전하기 전에 얻은 이미지 사이의 픽셀 대응 관계를 나타냅니다.
Image reprojection

3D의 reprojection이라기 보단 한 이미지에서의 다른 이미지로의
- 2D distortion
- 2D image warp
로 생각해볼 수 있습니다. 왜냐하면 두 평면에 대한 기하학은 어렵기 때문입니다.
Image reprojection

다시 이미지 재투영으로 돌아와 360 파노라마를 만들 때 homography를 사용할 수 있을지를 생각해본다면, No입니다.
왜냐하면 오른쪽으로 뻗어나온 검정색 선은 절대 projection plane에 닿을 수 없기 때문입니다.
Image warping with homographies

왼쪽 이미지는 앞을 보고 있고, 오른쪽 이미지는 아래 바닥을 보고 있습니다. 오른쪽에 보이는 검은색 공간(black area)은 pixel이 mapping 되지 않습니다. 위와 같은 예시라 볼 수 있습니다.
Unwrapping a sphere

이젠 이런 지구본을 이렇게 경도와 위도가 기준이 되는 직사각형 형태로 쫙 펴보는 unwrapping 방법을 살펴보려고 합니다.

Spherical projection

- 구에서 좌표 (r, theta, phi) 는 다음과 같이 정의 된다.
- r: 원점으로부터 P까지의 거리
- theta: z축의 양의 방향으로부터 원점과 P가 이루는 직선까지의 각
- phi: x축의 양의 방향으로 원점과 P가 이루는 직선을 xy 평면에 투영시킨 직선까지의 각
- 구를 평면으로 바꾸기 위해 unit sphere → unwrapped sphere → spherical image 로 변환하는 과정이 필요합니다
- 따라서 구면좌표계에서 직교좌표계로 변환하는 과정으로 이해할 수 있습니다.
- 구면좌표계에서 직교좌표계로 변환하기 위해 x, y, z가 저렇게 계산됩니다.
또한, r은 구의 반지름입니다. 여기서는 3D map 에서 sphere 위의 직교좌표계 point (X,Y,Z) 가 있고, √(X^2+Y^2+Z^2 )=R, 즉 sphere 중심에서 (X,Y,Z) 의 거리로 point (X,Y,Z) 에 나누어 sphere 위의 point 를 구할 수 있습니다.

Spherical reprojection
- Spherical coordinate 로 변환하려면 θ와 Ф를 이용해 나타냅니다.
- 마지막으로 spherical image coordinate 로 변환하려면 다음과 같은 형태를 갖는데, 해당 식에서 x_c와 y_c는 unwrapped sphere의 중심 point입니다.
- 식에서 s는 최종 이미지의 크기를 정의하며 scale factor 같은 역할을 합니다. 이미지 사이즈를 조절합니다. 또한, 이것은 camera focal length 로 설정하는 것이 편리하다고 합니다.
어떻게하면 구에서 평면 이미지로 mapping 할 수 있을까요?

image projection matrix를 사용하는 방법 또는 radial distortion을 계산하는 방법이 있습니다.

focal length (f)
focal length의 특징은 아래와 같습니다.
- focal length는 카메라에 따라 다르다.
- FOV를 측정하여 대략적인 추정값을 얻을 수 있다.
- 여러 이미지를 함께 사용하고, 일치 시킬 수 있는 f를 찾을 수 있다.
- 3D object와 projection을 사용하여 f를 해결할 수 있다.

focal length로 설정하는 것이 편리한 이유는 이미지를 spherical coordinates에 투영시킬 때 이 focal length에 따라서 달라지기 때문입니다.
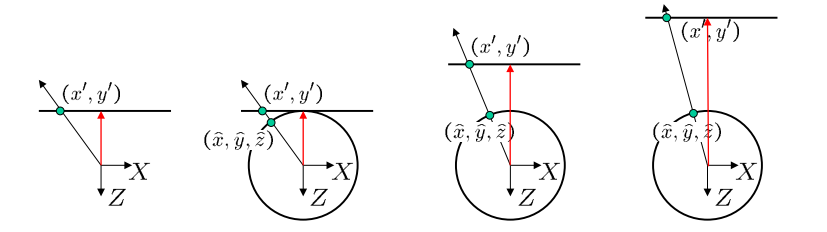
Aligning spherical images


- 수직 축에 대해 θ만큼 카메라가 회전한다고 가정하면, spherical image는 어떻게 바뀌나요?
- theta만큼 translation합니다
- 이것은 이미지를 translation하면서 spherical image를 align할 수 있다는 것을 의미
- 만약 카메라 회전을 모른다면 어떻게 되나요?
- 카메라 회전을 해석해야 합니다.
- 카메라의 회전은 구의 변환이라 볼 수 있습니다.
- spherical-warped images의 translation을 해결하기 위해 feature matching을 사용합니다.
Assembling the panorama
- Stitch, blend and crop

- Problem: Drift
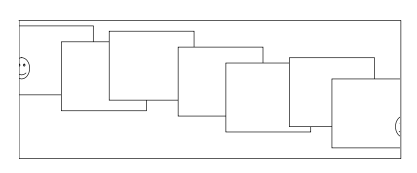
Drift의 문제는 Error accumulation(small errors accumulate over time)이라 볼 수 있습니다.
시간이 지나면서 작은 error들이 계속 누적되는 상황이고, 이로 인해서 matching이 잘못되는 경우를 말합니다.
이 방법을 해결하기 위해 bundle adjustment로 해결할 수 있습니다.
Solution

해당 부분은 더 공부한 다음에 따로 정리하려고 합니다,
Image Blending
- 이미지를 align한 다음은?

- aligned image를 서로 매끄럽게 합치기

그리고 이미지를 매끄럽게 합치기 위해 blending의 기법이 사용됩니다.
Alpha Blending
- alpha라는 불투명도를 결정하는 blending factor가 사용됩니다.
- Blend weight:

- Color at p:
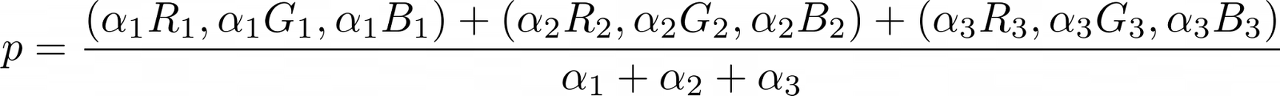

p의 식을 위의 이미지를 비교하면서 보면 대충 감이 오실 것 같은데요.
색상에 투명도 채널을 추가하여 (aR, aG, aB, a)라 쓰고, 픽셀의 불투명도를 조절할 alpha를 추가합니다. 불투명도는 얼마나 많은 빛이 통과하느냐? 의 관점으로 해석할 수 있으며, 투명도는 1-alpha로 주어집니다.
따라서 구현 방법과 a에 따라 달라지는 차이점을 살펴보려고 하는데요.
구현 방법
- accumulate: 각 픽셀에서 α를 미리 곱해둔 RGBα를 더해서 누적시킨다.
- normalize: 각 픽셀의 누적된 RGB 값을 각 α의 합으로 나눈다.
으로 아까 위의 식이 설명됩니다.
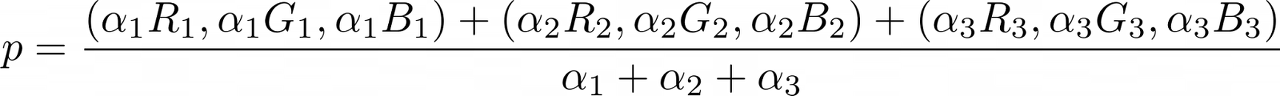
Q: what if α = 0?
- α = 1.0 - 완전 불투명
- α = 0.5 - 반투명
- α = 0.0 완전히 투명
저도 처음엔 좀 헷갈렸는데요.
α는 투명도를 결정하는 계수입니다. 그러므로 커질수록 투명해지고, 작을수록 불투명함을 의미합니다. 즉, α가 0이 되면 검정색으로 0%의 불투명도를 가지므로, 투명하다는 의미가 됩니다.
결론: α가 1이라면 불투명하게 되기 때문에 alpha blending은 의미가 없어집니다.
Image Blending

- 두 이미지를 서로 매끄럽게 합치는 것
- 이미지를 합칠 때 가중치를 두어 합치는 방법

한 이미지에 가중치를 높게 줄수록 해당 이미지는 진해지고, 다른 이미지는 흐려지는 효과를 의미합니다.
Feathering and window size
- feature의 가장자리를 부드럽게 하거나 흐리게 할 때 사용되는 기술

- 이미지를 블렌딩하기 위해 alpha mask를 사용하여 이미지를 부드럽게 만들어주어 합쳐졌습니다. 이를 feathering이라고 합니다.
- 왼쪽이 1, 오른쪽이 0인 가중치 값을 사용하면, 위와 같이 합쳐집니다.
- 중간 경계 부분인 transition area를 0과 1 사이의 어떤 값으로 만들어서 자연스럽게 합쳐주고 싶습니다.
- 그렇다면 어떻게 적당한 크기의 transition area를 설정해야 할까요?
이를 조절하는 것이 window size입니다.


- transition area의 크기
- 크면? 투명한 물체가 겹쳐보이는 효과 (ghosting)
- 좁으면? 경계선이 뚜렷해 보이는 효과
여기서 ghosting의 개념이 나옵니다. 가장 좋은 예시는 세 번째입니다.
이미지를 하나씩 살펴보면
- 세번째 window 이미지: “Optimal” window: smooth but not ghosted
- 뚜렷한 경계선을 피하고자 한다면 window의 크기를 가장 두드러지는 feature의 크기에 맞춰야 합니다.
- 반대로 ghosting을 피하고자 한다면, window의 크기를 가장 덜 두드러지는 feature의 크기에 맞추면 됩니다.
사실 이러한 규칙은 서로 모순됩니다.
만약 다른 크기의 특징이 여러군데 나타난다면 적절한 크기를 설정하는 것이 다소 어려울 수 있습니다.
이것이 alpha blending의 문제점이다. 이러한 문제는 어떻게 해결해야할까요?
Optimal Window

- seams를 피하기
- window = size of largest prominent feature
- ghosting을 피하기
- window <= 2 * size of smallest prominent feature
결론
- 뚜렷한 경계선을 피하고자 한다면, window의 크기를 가장 두드러지는 feature의 크기에 맞춰야 한다.
- 또한, ghosting을 피하려면 가장 작은 feature의 사이즈보다 두 배보다 작아야 한다.
이제 Blending의 방법을 몇 가지 살펴보고 마무리하겠습니다.
Pyramid blending
위의 문제를 해결하고자 multi-band blending의 해결 방법이 제안되었습니다.
- low frequency / high frequency component

- Low frequency component는 scale이 큰 개체를 가지고 있다는 것을 의미하고, 이 경우에는 넓은 transition window를 사용해서 seam을 피해야 합니다.
- 작은 개체에 대해서는 좁은 transition window를 사용해서 ghosting을 피해야 합니다.
- 이것을 기본 아이디어로, 2개의 pyramid가 있을 때,
- 높은 level은 low frequency에 해당해서 넓은 window를 사용
- 낮은 level은 high frequency에 해당해서 좁은 window를 사용
해야 합니다.
Laplacian Pyramid

- 각 이미지에 대해 2개의 Laplacian pyramid를 만듦
- region mask를 사용해서 pyramid로부터 각 level에서 blending하게 함
- 우리는 각각의 level마다 region mask가 필요하고, 이 mask는 alpha mask를 의미합니다.
- 마지막으로 최종 blended image를 얻기 위해서 pyramid를 겹칩니다.
Image 2개가 있다고 가정하겠습니다.
각각의 image에 대해서 Laplacian pyramid를 만들 수 있습니다. 각의 level에 대해서 alpha blending을 이용해서 2개의 image를 같이 blending을 진행합니다. 그러면 각각의 level에 대해서 1개의 blended image가 나옵니다. 그러면 Laplacian pyramid로부터 새로운 Gaussian image pyramid를 얻게 됩니다.
새롭게 image pyramid를 만들어졌고, 이를 계속 더해가면 최종적으로 output을 만들 수 있습니다. 가장 높은 level의 image를 upsampling해서 크기를 모두 같게 만듭니다.
여기까지 panorama의 내용을 정리하도록 하겠습니다! 혹시 내용에 틀린 부분이 있다면 지적 부탁드립니다. 감사합니다.
'AI > Computer Vision' 카테고리의 다른 글
| [보충] Camera model and Vanishing points (0) | 2022.08.09 |
|---|---|
| [CS5670] Lecture 12: Single-view modeling (0) | 2022.08.09 |
| [CS5670] Lecture 10: Cameras (2) (0) | 2022.07.18 |
| [CS5670] Lecture 10: Cameras (1) pinhole, lens camera (0) | 2022.07.18 |
| [보충] Affine transformations and Homography (0) | 2022.07.14 |




댓글