티스토리 뷰
이번 포스팅에서 정리할 내용은 Camera models와 vanishing points와 관련된 내용입니다. 자료는 모두 아래 링크를 바탕으로 정리한 내용임을 밝힙니다.
참고 자료: [Multiple View Geometry in Computer Vision 책 내용 정리 Part 1]



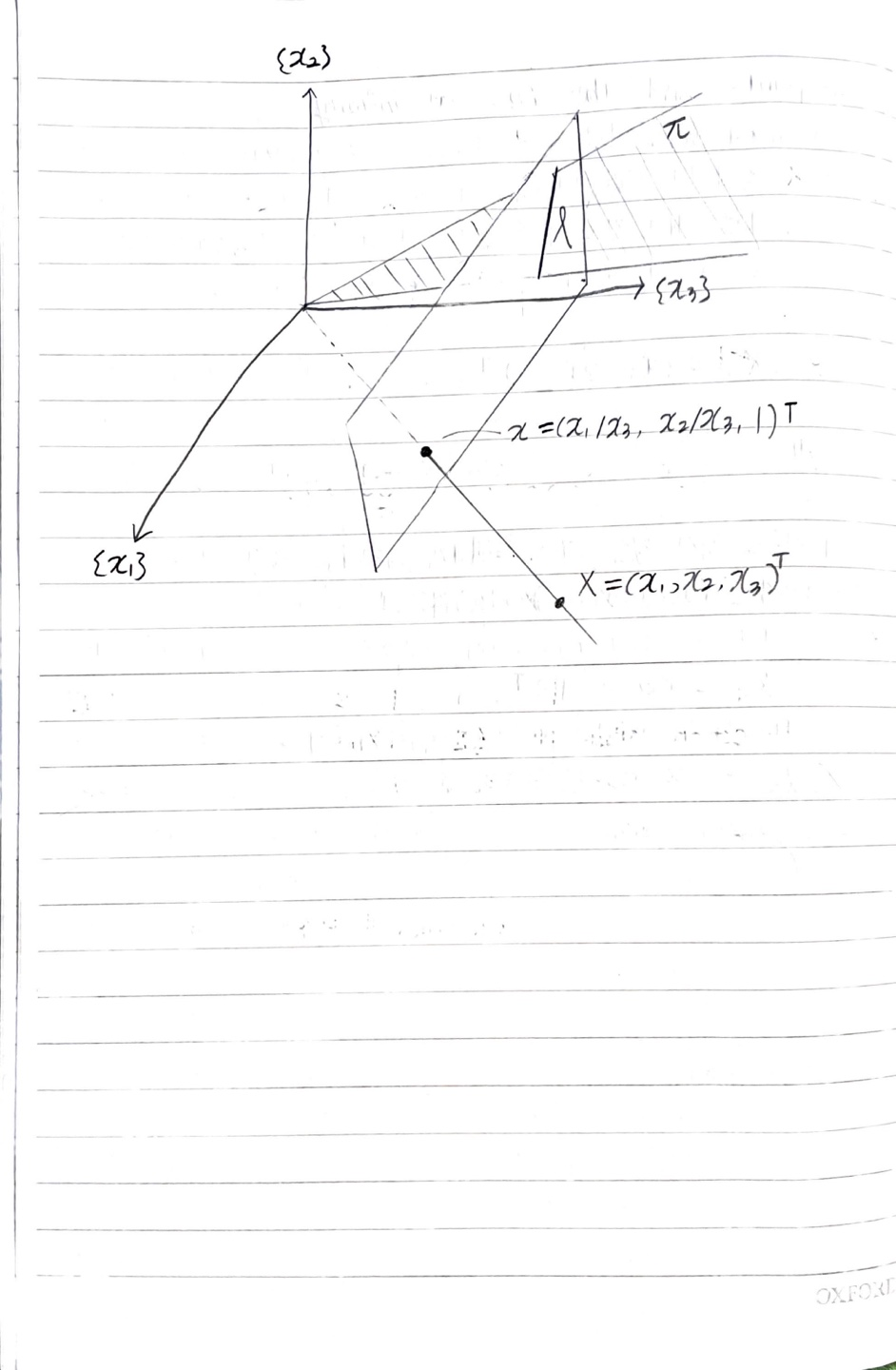
Camera model에 대한 내용입니다.
pinhole model, principal pount offset, intrinsic parameter matrix, camera calibration matrix에 대한 내용이 나옵니다.






이제 projective camera에 대한 내용 정리를 하며 vanishing points 관련 내용까지 정리해보려 합니다.
카메라 행렬 P에 대해 정리를 했었는데요. 카메라 행렬 P를 column, row vector로 나타낼 수 있습니다.
→ 카메라 행렬 P는 P3 공간 상의 점 X를 P2 공간 상의 점 x로 projection하는 선형사상을 의미합니다.
Column vectors
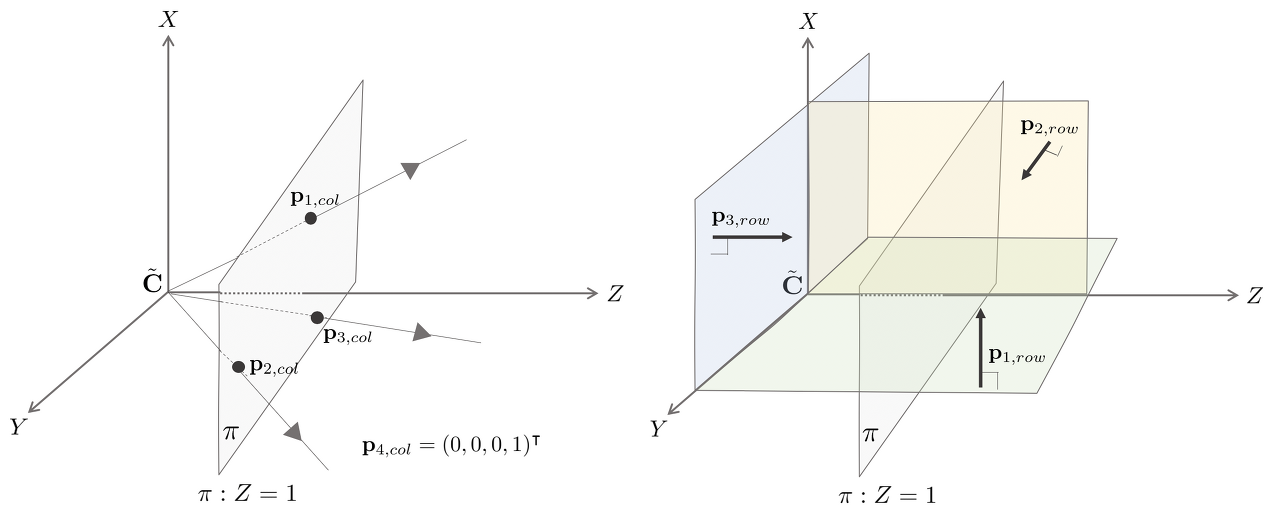
왼쪽과 오른쪽 그림을 하나씩 살펴보겠습니다.
왼쪽 그림은 column vector의 경우에 해당합니다. 그리고 위 모델은 basic pinhole model로 볼 수 있습니다.
camera center C에서 이미지 평면 π로 뻗어나온 직선 [P1,col,P2,col,P3,col이 있고, P4,col=(0,0,0,1)T가 있습니다.
카메라 행렬 P를 열벡터(column vector)로 나타내면 다음과 같습니다.
P=[P1,col,P2,col,P3,col,P4,col
where,Pi,col∈R3×1,i=1,…,4
이중 Pi,col,i=1,2,3,4는 각 무한대 평면 π∞에 위치한 X,Y,Z 축의 소실점(vanishing point)들의 위치를 의미합니다.
P4,col=P(0 0 0 1)T은 월드 좌표계의 원점을 의미합니다.
되게 간단한 부분인 것 같은데 이해가 안 돼서 더 찾아본 결과, Multiple View Geometry 책에는 이렇게 설명되어 있다고 합니다.

위 내용을 그대로 해석해보겠습니다.
projective camera의 열은 특정 이미지 점으로의 기하학적 의미를 갖는 3 vectors입니다. 이 점은 vanishing point를 의미하고 있는 것 같습니다. 따라서 P의 열이 pi,i=1,…,4로 표현되고, p1,p2,p3는 각각 월드 좌표 X, Y, Z축의 vanishing point입니다.
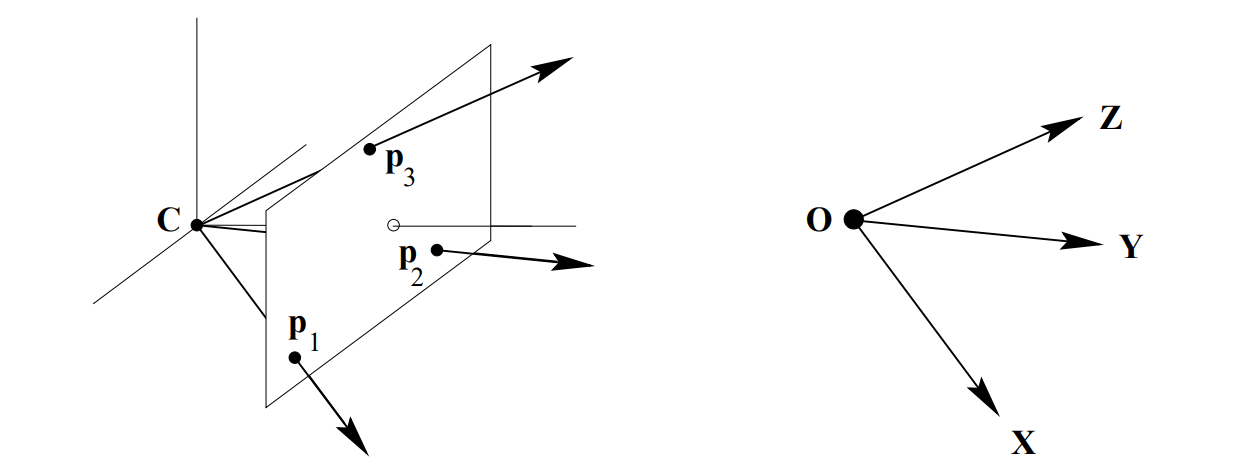
무한대 점(point at infinity)은 평행 선들의 공통 교차점입니다. P는 선의 교차점을 유지하므로 그 이미지는 소실점이라 볼 수 있습니다.
무한대에서 이 점의 homogeneous coordinates는 0이 추가된 선의 homogeneous의 방향 벡터를 의미합니다. 예를 들어, X축의 무한대 점은 homogeneous coordinates X1=(1,0,0,0)T를 갖습니다.
p1=PX1
Row vectors
위 이미지의 오른쪽이 row vector에 해당됩니다.
카메라 행렬 P를 행벡터(row vector)로 나타내면 다음과 같습니다. 카메라 행렬 P가 3×4 크기이므로 3개의 row vector로 구성될 수 있습니다.
P=[PT1,rowPT2,rowPT3,row]
where, pi,row∈R4×1, i=1,2,3
행벡터 pi,row, i=1,2,3은 카메라 좌표계 기준으로 각 X,Y,Z 축과 평행한 평면을 의미합니다.
The principal plane
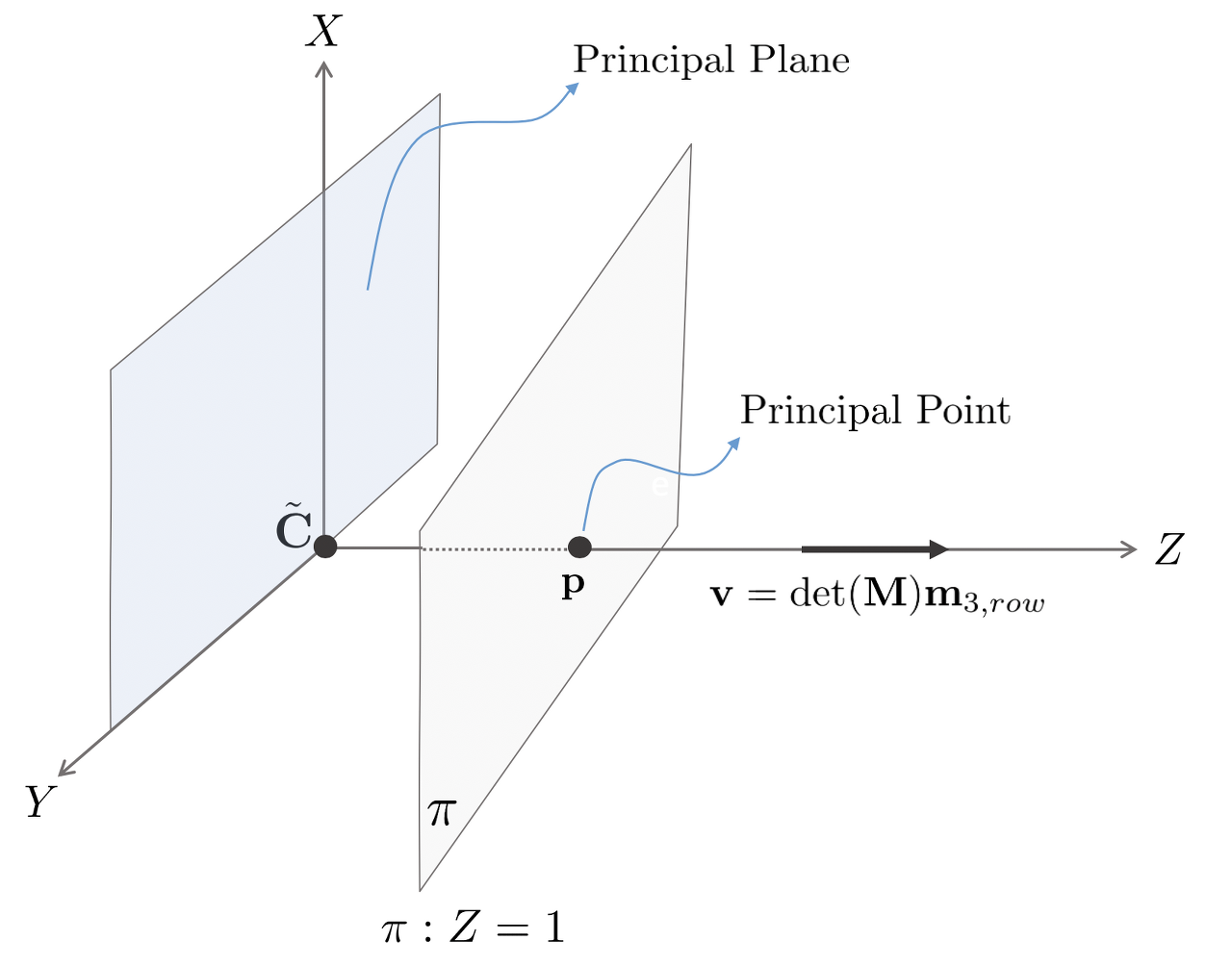
주평면(principal plane) πpp은 카메라의 중심점(center)를 포함하며 이미지 평면과 평행인 평면을 의미합니다.
주평면은 카메라 좌표계 C에서 XY 평면과 동일하며 Z=0인 특징이 있습니다. 주평면 상에 위치하는 한 점 X∈πpp는 무한대 선(line at infinity) 상에서 이미지 평면 π와 만납니다.
x=PX=(x y 0)T
만나는 지점의 x 좌표는 위와 같습니다.
따라서 임의의 한 점 X가 주평면 상에 위치하기 위한 필요충분 조건은 PT3,row=0입니다. 즉, 카메라 행렬의 세 번째 행벡터 P3,row가 곧 카메라의 주평면을 의미합니다.
The principal point
주점(principal point) p는 주축(principal axis)와 이미지 평면 π의 교차점을 의미합니다.
주점 p는 이미지 평면 π 상에 위치하며 카메라 중심점 C와 주점을 잇는 직선은 이미지 평면과 수직하게 됩니다.
p−C⊥π
또한, 주평면은 카메라 행렬의 세 번째 행벡터 p3,row이므로 주평면 상에 위치한 점 X에 대해
pT3,rowX=0
이와 같이 성립합니다.
이때 세 번째 row vector p3,row=(π1,π2,π3,π4)T는 Dual Projective Space P3에서 p3,row 평면의 법선벡터를 의미합니다.
주평면 p3,row와 무한대 평면(plane at infinity) π∞의 교차선은 무한대 평면에 존재하는 법선벡터 (π1 π2 π3 0)T가 됩니다.
결론적으로 이를 이미지 평면으로 projection한 점이 주점(principal point) p가 됩니다.
p=P(π1π2π30)
즉, 카메라 중심점 C를 지나면서 무한대 평면 상에 존재하는 법선벡터 [π1 π2 π3 0]T는 곧 주축(principal axis)과 같아서 주축을 이미지 평면에 프로젝션하면 주점 p가 됩니다.
결론적으로 주점 p는 카메라 행렬 P의 세 번째 행벡터 p3,row=(π1,π2,π3,p4)T에서 처음 세 개의 항 p=(π1π2π3)T을 의미합니다.
위의 과정은 월드 상에 있는 한 점 X가 주어졌을 때, 이를 이미지 평면 상의 한 점 x로 변환하는 연산을 의미합니다. 따라서 해당 식이 성립합니다.
x=PX
감사합니다.
'AI > Computer Vision' 카테고리의 다른 글
| [CS5670] Lecture 14: Light & Perception (0) | 2022.08.16 |
|---|---|
| [CS5670] Lecture 13: Stereo (0) | 2022.08.10 |
| [CS5670] Lecture 12: Single-view modeling (0) | 2022.08.09 |
| [CS5670] Lecture 11: Panoramas (0) | 2022.08.08 |
| [CS5670] Lecture 10: Cameras (2) (0) | 2022.07.18 |
- Total
- Today
- Yesterday
- few-shot learning
- 파이썬 딕셔너리
- prompt learning
- 구글드라이브서버연동
- 구글드라이브서버다운
- 프롬프트
- style transfer
- docker
- 서버에다운
- 구글드라이브다운
- NLP
- 도커 컨테이너
- clip
- 딥러닝
- python
- vscode 자동 저장
- 도커
- CNN
- Unsupervised learning
- 파이썬 클래스 계층 구조
- 서버구글드라이브연동
- 구글드라이브연동
- Prompt
- 파이썬
- support set
- 데이터셋다운로드
- 퓨샷러닝
- stylegan
- cs231n
- 파이썬 클래스 다형성
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

