티스토리 뷰
해당 게시글은 제가 뭘 모르는지도 잘 모르는 채 일단 정리합니다. 혼자 공부하며 정리한 내용이다 보니 오류가 있을 수도 있는데 발견시 지적해주시면 정말 감사드리겠습니다.🤦♀️
Intro
이미지/영상 작업에 있어 Transformation은 기본적인 이미지 처리 방법인 filter나 blurring 등의 적용을 의미합니다. 픽셀 단위 별로 변환을 주는 작업에 해당됩니다. 특징으로는 픽셀 값의 변화가 있을 뿐, 픽셀의 위치 이동은 없다는 점입니다.
여기서 Geometric transformation이란 영상을 구성하는 픽셀이 배치된 구조를 변경함으로써 전체 영상의 모양알 부끄는 작업을 뜻합니다. 즉, 어떤 픽셀의 좌표가 다른 좌표로 이동되는 경우를 의미합니다.
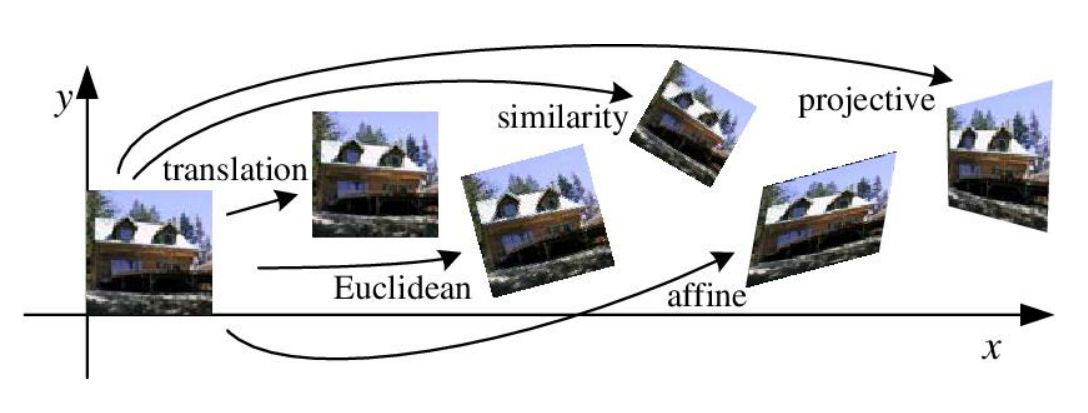
위 그림은 대표적인 geometric transformation의 예시를 보여줍니다.
| Translation, Euclidean, Similarity, Affine, Projective
등이 있으며, 이중에서 Homogeneous coordinates(동차좌표계)를 설명하여 affine 변환과 projective 변환에 대해 더 공부하며 정리해볼 예정입니다.
Homogeneous coordinates

포인트의 transformation과 벡터의 transformation을 한 번에 표현하는 transformation matrix를 구하는 방법입니다.
N차원 벡터와 포인트를 표현할 때, N+1 차원의 벡터와 포인트를 사용하게 됩니다.

- 포인트를 나타날 때, 마지막 차원의 값이 0이 아닌 경우 모든 포인트 의미를 가지기 때문에 homogeneous 좌표 표현은 무한히 많이 존재하게 됩니다.
- 따라서 벡터의 경우, 추가된 차원에 0을 사용하고 포인트의 경우, 추가된 차원에 1을 사용합니다.
- 이와 같은 형태로 transformation matrix를 사용하게 되면 벡터와 포인트에 대하여 linear transformation과 translation을 하나의 transformation matrix로 표현할 수 있습니다.
정리하자면,
- Translation을 하나의 transformation matrix로 표현 가능
→ 벡터와 포인트를 같이 표현할 수 있는 좌표계
해당 성질을 이용하여
- Affine/Perspective Transform 형태를 행렬곱 형태 y = Ax (Linear Transformation)로 나타낼 수 있음
- Affine/Perspective Transform이 연속적으로 발생하더라도 Linear Transformation 형태로 나타낼 수 있음
Affine transforation
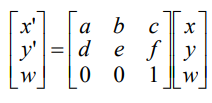
- Affine transformation are combinations of …
- Linear transformation + Translation (rotation, translation, scaling, shearing 등을 모두 포함한 변환)
- 2x3 matrix
- 6개의 parameter (DOF, Degree of Freedom, 자유도)
DOF를 통하여 자유롭게 변형이 이미지의 기하학적 변환이 가능하기 때문에 자유도와 같은 이름으로 불립니다. 위 변환 행렬에서 2 X 3 행렬 크기의 파란색 음영의 6개 DOF가 정해지면 그 값에 맞춰서 이동, 전단, 크기, 대칭, 회전 등의 변환을 하게 됩니다.
Affine transformation(아핀 변환)의 특징으로는
- Properties of affine transformations:
- Origin does not necessarily map to origin
- Lines map to lines
- Parallel lines remain parallel
- Ratios are preserved
- Closed under composition
이동을 하기 때문에 원점이 유지 안 되고, 나머지는 2D linear transformation이 갖고 있는 특징과 같습니다.
선 그대로 매핑이 된다는 점, 평행선이 유지된다는 점, 비율도 유지 되고, 연속적인 연산이 가능합니다.
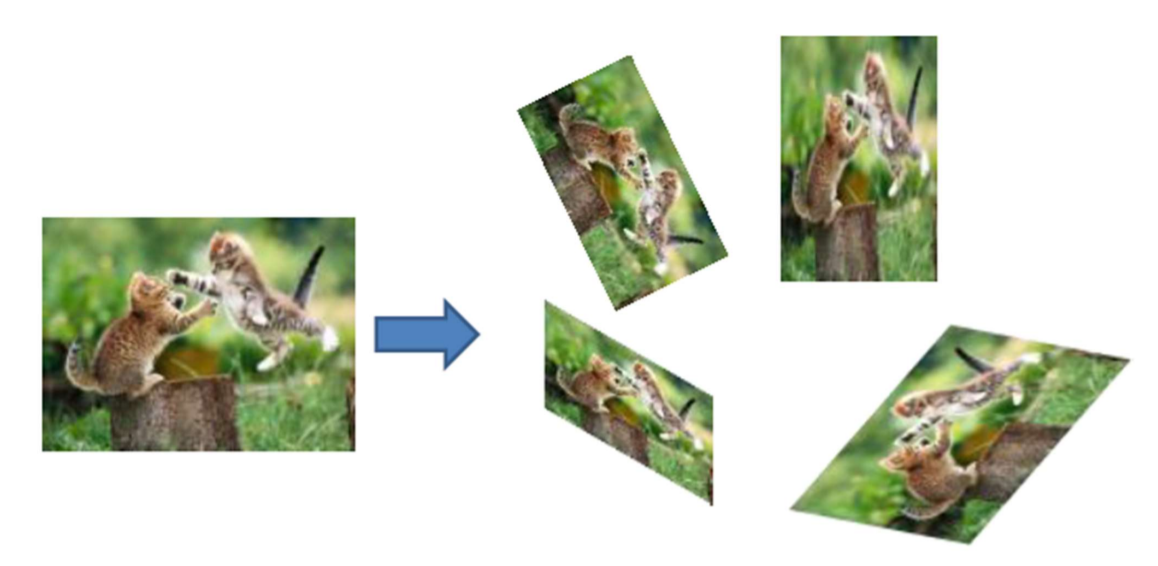
해당 특징을 위 이미지랑 빗대어 비교해 볼 수 있습니다!
Projective transforation(Homographies)
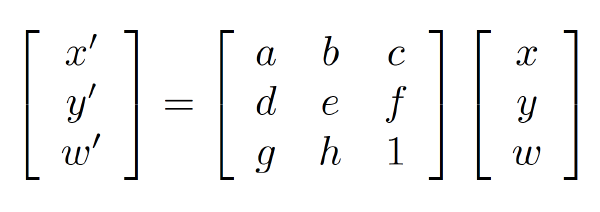
- Homographies …
- Affine transformations + Projective warps
- 3x3 matrix
- 8개 parameter
한 평면을 다른 평면에 Projection(투영) 시켰을 때, 투영된 대응점들 사이에서는 일정한 변환 관계가 성립합니다. 이 변환 관계를 Homography라고 하는데요. 비스듬한 각도를 transformation해서 정면에서 찍은 것처럼 변환해줍니다.
저는 스캔 어플을 예시로 생각했을 때 가장 잘 이해가 되었는데요. 어떻게 찍어도 정면에서 찍은 것처럼 PDF나 Image로 변환시켜주는 경우에 해당되는 것 같습니다.
Perspective Transformation을 적용하기 위해서는 두 이미지 간의 관계를 설명해주는 matrix 계산이 필요합니다.
즉, 각각의 픽셀을 특정한 위치로 이동시켜주는 행렬을 구합니다. Perspective Transformation에서는 3 X 3 행렬에서 파란색 음영의 8개 DOF가 정해지면 그 값에 맞춰서 변환을 하게 됩니다. 적어도 4개의 corresponding pair가 주어져야 계산을 할 수 있습니다.
특징으로는
- Properties of projective transformations:
- Origin does not necessarily map to origin
- Lines map to lines
- Parallel lines do not necessarily remain parallel
- Ratios are not preserved
- Closed under composition
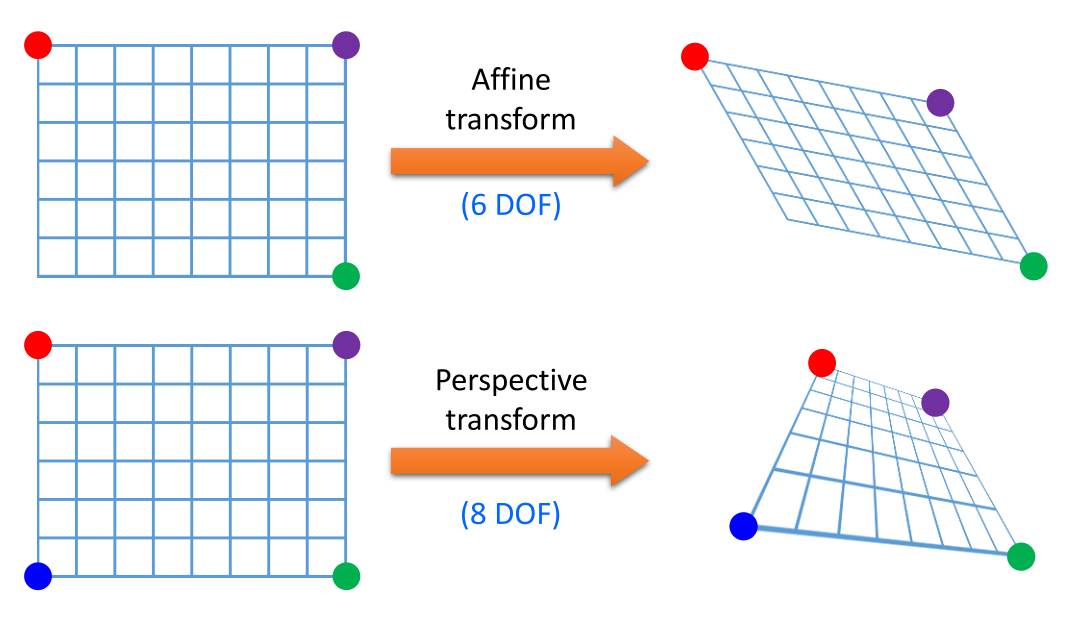
위와 같은 특징이 있으며, 평행선이 유지되지 않는다는 점이 Affine transformation과 차이점입니다.
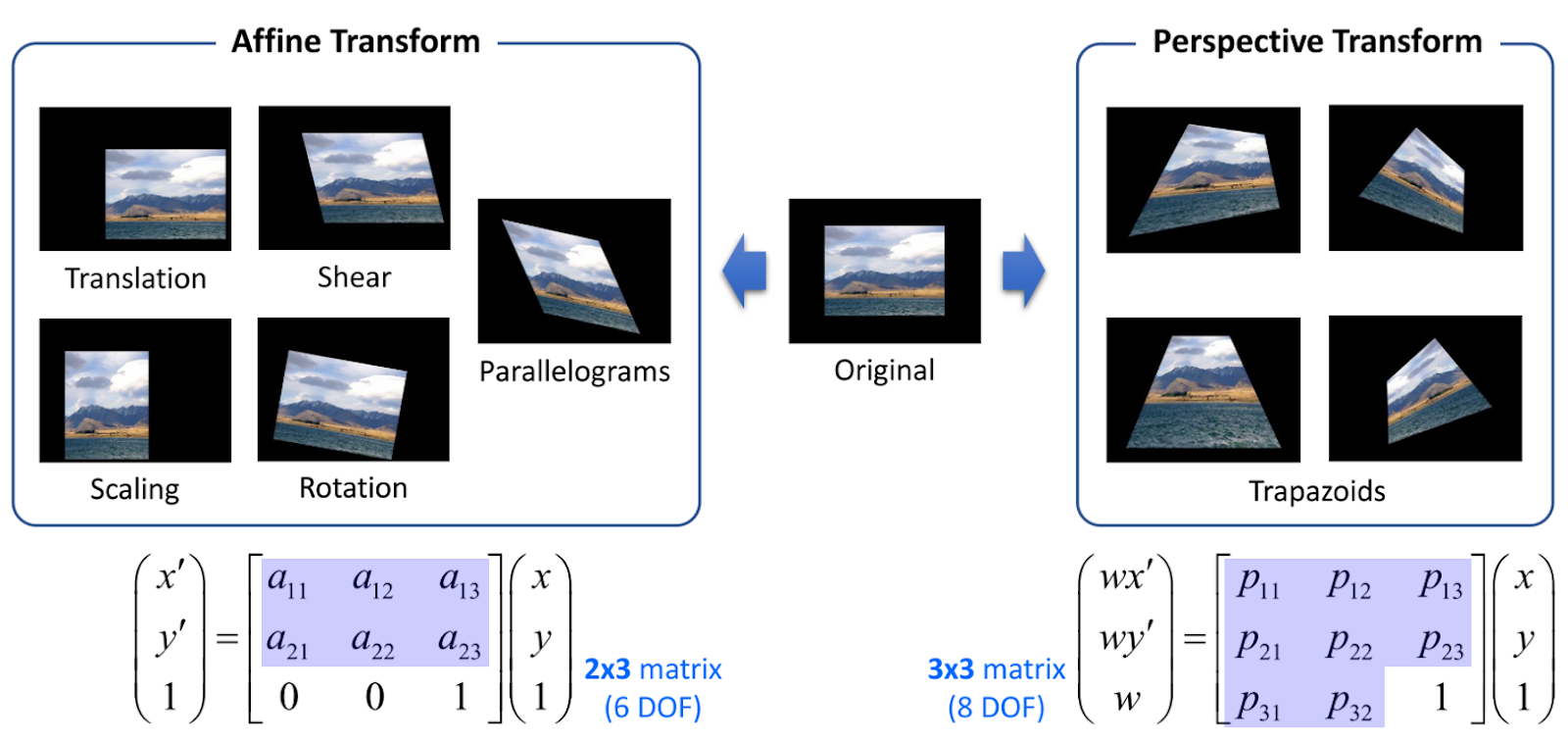
두 변환을 비교해보면 이렇습니다.
여기까지가 기본적인 개념이고, 해당 변환 등을 계산하기 위한 matrix form을 통해 연산하는 과정을 더 살펴보려고 합니다.
제가 이해하고 싶은 부분은 아래 부분이고, 다음 포스팅에 이어 해보겠습니다.

Reference
'AI > Computer Vision' 카테고리의 다른 글
| [CS5670] Lecture 10: Cameras (2) (0) | 2022.07.18 |
|---|---|
| [CS5670] Lecture 10: Cameras (1) pinhole, lens camera (0) | 2022.07.18 |
| [CS5670] Lecture 7: Transformations and warping (0) | 2022.06.24 |
| [CS5670] Lecture 6: Feature Descriptors and Feature Matching (0) | 2022.06.23 |
| [CS5670] Lecture 5: Feature Invariance (0) | 2022.06.23 |
- Total
- Today
- Yesterday
- 서버구글드라이브연동
- 파이썬 클래스 다형성
- 도커
- 딥러닝
- cs231n
- Unsupervised learning
- NLP
- clip
- docker
- support set
- 파이썬
- 리눅스 nano
- 리눅스 나노
- few-shot learning
- 파이썬 클래스 계층 구조
- style transfer
- 파이썬 딕셔너리
- 구글드라이브연동
- linux nano
- CNN
- stylegan
- 도커 컨테이너
- python
- 퓨샷러닝
- 리눅스 나노 사용
- 도커 작업
- 리눅스
- Prompt
- 프롬프트
- prompt learning
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

