강의 참고 자료: CS5670 Lec 12
이번 강의는 single-view modeling에 대한 내용입니다.
가장 주요하게 다루는 내용은 vanishing point와 line이며 이를 통해 무엇을 계산하고 얻을 수 있는지, 또 계산 방법은 어떻게 되는지에 집중을 하면 좋을 것 같습니다.
Ames Room

착시를 이용한 공간으로 멀리 있는 물체는 작게, 가까이 있는 물체는 크게 인식하도록 하였습니다.
- A의 원래 자리와 A의 보이는 자리가 다르고 B는 같습니다.
- 우리가 보는 틈새 구멍으로 착시가 발생합니다.
Point and line duality

- 여기에 점과 직선이 있는데, homogeneous notation을 통해 평면 위의 점과 직선에 대해 하나의 동일한 벡터로 표현할 수 있습니다.
- 이러한 관계를 equivalent(동치 관계)에 있다고 하며, 이 관계에 있는 모든 벡터를 homogeneous vector라 합니다.
이렇게 homogeneous 관계에 두면서 표현하는 이유는
- 첫 번째로 카메라 초점과 카메라 영상의 픽셀점을 이어 ray를 만들면 그 ray에 존재하는 모든 점을 동차좌표 하나로 표현할 수 있기 때문
- 두 번째로는 소실점과 같은 실제 세계에서 무한대를 나타내는 점을 2D에서 표현할 수 있어서 기하학적 계산을 할 때 편리해서
입니다. 이 소실점은 z=0으로 나타낼 수 있습니다.
Points and lines


- 직선 $l$ 위에 임의의 한 점 $x=(x,y,1)$이 존재하면 $ax+by+c=0$의 공식에 따라 $l$을 $(a,b,c)$로 표현할 수 있습니다.
- 직선 $l$과 직선 위의 한 점 $x$ 사이에는 다음과 같은 공식이 성립합니다.
- 두 벡터 $l$과 $x$의 내적으로 표현이 가능합니다.
- 직선 위의 한점 $x=(x,y)$ 좌표 끝에 1을 추가하여 직선과 내적하였습니다.
Homogeneous representation of points
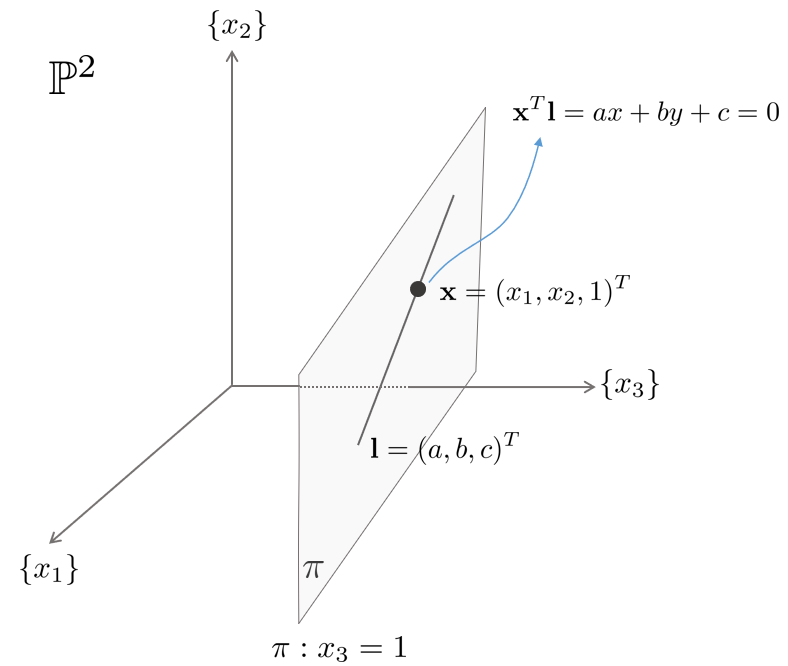

따라서 다시 그림으로 표현하면 왼쪽과 같고, 평면 공간 상에서 임의의 한 점 x가 직선 l 위에 존재할 경우 오른쪽과 같이 공식이 성립합니다.
Intersection of lines
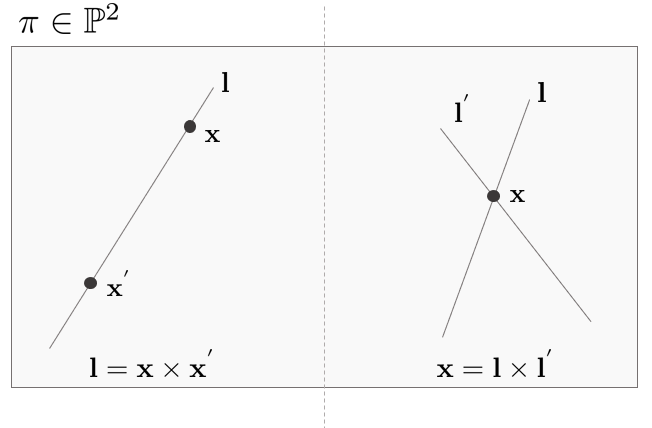
- 두 직선의 방정식$x^T I^\prime = 0$
- $x^TI = 0$
- 교차점
- $x = l \times l^\prime$
- 공간 상의 두 개의 직선이 주어졌을 때, 두 직선의 방정식을 표현합니다.
- 이때 교차점 $x$는 스케일 값에 관계없이 하나의 점을 의미하므로 두 직선의 cross product의 배수로 나타낼 수 있습니다.
- 두 직선의 교점을 구하는 공식과 유사하게 두 점 $x, x^\prime$이 주어졌을 때, 두 점을 지나는 직선 l은 다음과 같이 구할 수 있습니다.
Ideal points and the lines at infinity
- Point at infinity
- $x_\infin = (x_1 \ x_2 \ 0)^T$
- Line at infinity
- $l_\infin = (0 \ 0 \ 1)^T$
- 따라서 다음이 성립
- $x_\infin^T I_\infin = (x_1 \ x_2 \ 0)(0 \ 0 \ 1)^T = 0$
- 두 직선 $l, l^\prime$이 평행한 경우 두 직선의 교차점은 $R^2$ 공간에서는 만나지 않지만 $P^2$ 공간에서는 만납니다. (R: 유클리디안 공간, P: projective space, 사영 공간)
- 평행한 두 직선은 무한대에 위치한 점 x에서 교차하므로 x = l × l’ 공식이 성립합니다.
- 무한대 점 x를 $R^2$ 공간으로 변환하면 (b/0, -a/0)이 되어 유효하지 않는 점으로 변환되고, 따라서 $P^2$ 공간에서 무한대 점 $x = (x,y,0)^T$는 $R^2$ 공간으로 변환되지 않습니다.
- 무한대 점들은 특정한 직선 위에 존재하게 되는데 이런 직선을 무한대 직선(line at infinity)라고 합니다.
- 이전의 설명과 같이 두 평행한 직선 l, l’은 무한대 점에서 교차한다는 것을 알 수 있으며, 유클리디안 공간에서는 평행한 직선들이 서로 교차하지 않지만, 사영 공간에서는 서로 다른 두 직선은 반드시 한 점에서 교차한다는 점을 알 수 있습니다.
Question

Consider the above image, with four points p, q, r, s labeled (assume these are 2D homogeneous points).
What is a simple expression for the point of intersection between the line through p and r and the line through q and s?
point p와 r이 있는 line과 q와 s가 있는 두 라인으로 만들어지는 교차점은 위의 식대로 구할 수 있습니다.
정리
두 점을 지나는 직선 $l$과 $l^\prime$을 두 점의 곱으로 표현할 수 있고, 또 두 직선을 곱하면 교차점을 구할 수 있기 때문에 이렇게 답이 유도됩니다.
Duality

- 공간에서 점과 직선이 대칭성(duality)를 가집니다.
- 점과 직선이 동일한 공식에 대해 위치를 바꾸어도 성립합니다.
- 즉, 두 점을 통과하는 직선의 공식은 두 직선이 교차하는 한 점의 공식과 대칭입니다.
직선 위의 한 점과 두 직선이 교차하는 한 점은 두 가지 방식으로 표현이 가능합니다.
Ideal points and lines

- 무한대점(point at infinity) 또는 ideal point라고 합니다.
- 무한대 직선(ideal line)은 직선이 이미지 평면에 평행한 경우를 의미합니다.
- 이 직선은 이미지 원점을 통과하고, 유한한 좌표인 이미지의 선에 해당합니다.
- 같은 경우는 무한대 점들이 특정한 직선 위에 존재하게 되는데 이러한 직선을 의미합니다.
3D projective geometry

These concepts generalize naturally to 3D
- Homogeneous coordinates
- Projective 3D points have four coords: P = (X,Y,Z,W)
- Duality
- A plane N is also represented by a 4-vector
- Points and planes are dual in 3D: N P=0
- Three points define a plane, three planes define a point
이 개념은 보통 3D에서 일반화됩니다.
- 3D projective은 4개의 좌표 값을 가집니다.
- 마찬가지로 4개의 벡터로 평면 N이 표현되고, 점과 평면이 대칭됩니다.
- 세 점은 평면에 정의되고, 세 평면은 점에 정의됩니다.
3D to 2D: perspective projection
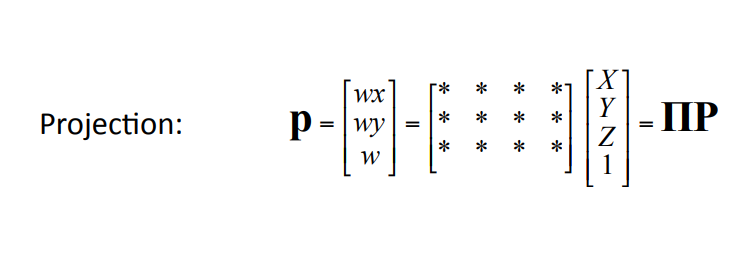
행렬 P는 Homogeneous point를 옮기는 것으로 생각할 수 있습니다.
카메라 행렬 P는 내부 파라미터와 외부 파라미터로 이루어진 행렬로 표현이 되었습니다.
Vanishing points and lines


- 평면에 있는 평행선의 집합 → vanishing point
- 이 모든 소실점의 집합은 horizon line (vanishing line)
- 다른 평면은 다른 소실선을 정의할 수 있음
무한대의 점에 투영하는 것 (ideal points in 2D)이라 볼 수 있습니다. 종종 이미지의 유한한 점으로 투영할 수 있습니다. 그런데 항상 그런 것은 아닙니다. (points where parallel lines intersect in 3D)
Vanishing points


- 모든 선들은 같은 vanishing point에 같은 방향을 갖고 있습니다.
- C에서 V까지의 선은 두 선과 평행합니다.
- 이미지에는 소실점이 하나 이상 있을 수 있습니다. (모든 이미지의 점은 잠재적 소실점)
Vanishing point가 갖는 특성을 읽으며 이해해보시길 바랍니다!
- line on the ground plane에 위치하는 파란색 점들이 image plane으로 투영될 때 점점 vanishing point로 수렴하는 걸 볼 수 있습니다.
- 현재는 광학축 (camera 좌표계에서 z축)이 평면의 파란색 선과 평행하기 때문에, 광학축이 영상 평면과 교차되는 점으로 vanishing point가 나타납니다.
- 두 개의 평행선은 동일한 소실점을 갖습니다. 두 개가 아니더라도 3D에서 평행한 직선은 모두 동일한 소실점을 갖습니다.
- C에서 V까지의 선은 두 선과 평행합니다.
- 이미지에는 소실점이 하나 이상 있을 수 있습니다. 실제로 모든 이미지의 점들은 잠재적인 소실점이라 볼 수 있습니다.
Vanishing lines

- 평행한 평면에 속한 직선들의 소실점들은 모두 일직선
- 상에 존재 → Vanishing line
- 두 평면이 서로 평행이면 이들은 동일한 소실선을 가짐
- 다른 평면은 다른 소실을 정의함
- 기하학적으로봤을 때, 어떤 평면에 대한 소실선은 이 평면과 수평이고 카메라 원점을 지나는 평면이 이미지 평면과 만나서 생기는 교선이라 볼 수 있음
평면에 있는 모든 평행한 선은 소실점을 만듭니다. 소실점의 위치를 결정하는 것은 직선의 방향이기 때문입니다. 그리고 이처럼 평행한 평면에 속한 직선들의 소실점들은 모두 일직선 상에 존재하게 됩니다.
이 모든 소실점의 합을 수평선, vanishing line이라고 부릅니다. 다른 평면은 다른 소실을 정의할 수 있습니다.
One/Two/Three-point perspective

소실점의 갯수에 따라 경우가 이렇게 나뉩니다.
Computing vanishing points
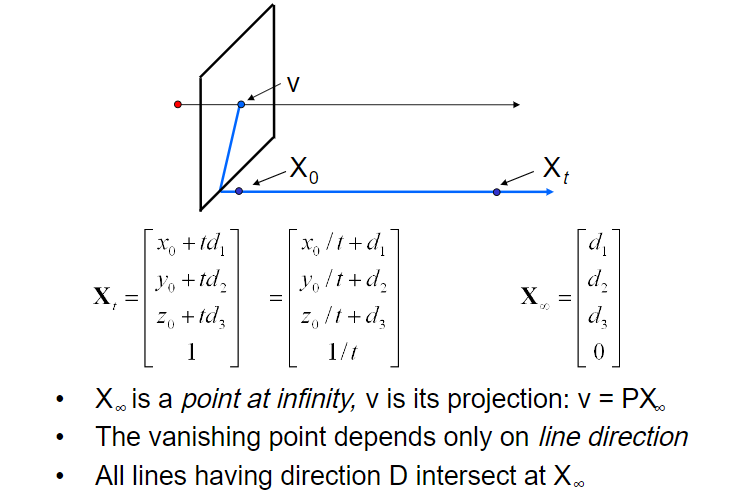
3D에서 방향 D를 가진 점 $x_0$을 지나는 점의 선 $X_t$를 homogeneous 로 표현한다면 다음과 같습니다.
따라서 t를 무한대로 보내면 $X_\infty$는 오른쪽 식과 같이 나타납니다.
$X_\infty$는 즉, point at infinity이며, v는 그것에 사영한 것입니다. 그래서 v는 $PX_\infty$로 나타낼 수 있습니다.
- vanishing point는 직선의 방향에 의존합니다.
- 모든 선은 $X_\infty$와 교차하는 방향 $D$를 가집니다.
- t는 직선 위에 존재하는 점들을 의미, 이미지 평면에 projection한 점을 의미합니다.
Computing vanishing lines
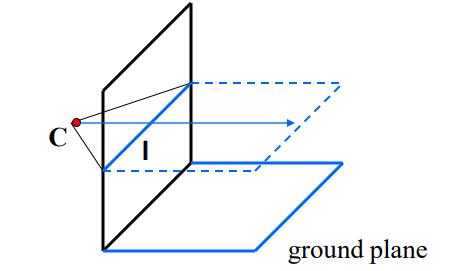
- Line l은 이미지 평면과 C를 통한 수평 평면의 교차점입니다
- Ground plane에 있는 두 개의 평행선 세트에서 l을 계산할 수 있습니다
- C와 같은 높이의 모든 point들은 l에 project 됩니다
- Scene에서 object의 높이를 비교하는 방법을 제시합니다
Computing vanishing points (from lines)


Measuring height

- Compute Z from image measurements
- Need more than vanishing points to do this
문제는 카메라 각도와 거리가 매번 다르다는 점입니다. 따라서 불변하는 특징을 이용해서 계산합니다.
The cross ratio

- Projective Invariant → 3D heights와 연관
- 동일선상 점의 교차비는 projective transformation에서 변하지 않음
- 점 중 하나가 소실점인 경우, 3D 위치는 무한대이므로 비율을 단순화함
- 수직 소실점을 이용하면 scene에서 object의 상대적 높이를 구할 수 있음
Perspective projection을 포함한 Project transformation에서 변하지 않는 것을 projective invariant 하다고 합니다. 다음과 같이 4개의 동일선상의 cross ratio 는 다음과 같은 수식으로 표현 합니다.
Measuring height


Ground plane 에서 높이를 측정할 때의 예시입니다. Scene cross ratio 와 image cross ratio 는 다음과 같이 동일합니다. projective invariant한 cross ratio가 같은 특성을 이용하였습니다. 동일한 ray 위에 있는 point 이면서 동일한 vanishing point c 로 이어집니다.
- R: reference point
- T: top of object
- B: bottom of object
- ground plane
여기서 길이 H를 한 번 구해보세요. 전 머리가 없어서 헤맸습니다…
아래 과정을 통해 구할 수 있습니다.
- $V_x-V_y$는 horizon이다.
- $b_0, b$은 한 line1 으로 연결
- line 1과 점 $v$에서의 수평은 교차한다
- $v$와 $t_0$은 line 2로 연결
- line2와 점 $t$에서의 $r-b$ 수평선은 교차한다
- 이 공식을 통해 계산한다.
Related problem: camera calibration
- Goal: estimate the camera parameters
- Version 1: solve for 3x4 projection matrix
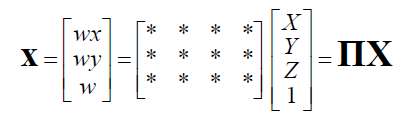
- Version 2: solve for camera parameters separately
- intrinsics (focal length, principal point, pixel size)
- extrinsics (rotation angles, translation)
- radial distortion
camera calibration 의 문제를 푸는 두 가지 방법이 있었습니다. 목표는 카메라 파라미터를 추정하는 것이었습니다.
- 3x4 projection matrix를 푼다.
- camera parameter를 분리해서 푼다.
Vanishing points and projection matrix
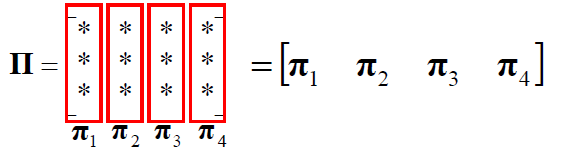
- p1은 x 방향의 vanishing point이며, p2, p3도 마찬가지
- p4는 월드 좌표계의 원점에 투영함

- projection matrix를 column 기준으로 나누어 파이1, …, 파이4로 나타냅니다.
- 파이1, 2, 3은 각 x, y, z의 vanishing point를 표현합니다. (why? 이 부분에 대한 이해가 부족해서 따로 공부해서 포스팅하려고 합니다.)
- 처음 세 열은 투영 행렬과 같고 네 번째 열은 이미지 좌표의 world origin입니다.
- 즉, projection matrix는 다음과 같이 vanishing point로의 표현이 가능합니다.
Calibration using a reference object

- Place a known object in the scene
- identify correspondence between image and scene
- compute mapping from scene to image

Issues
- must know geometry very accurately
- must know 3D → 2D correspondence
여기까지 single-view modeling에 대한 내용 정리를 마치겠습니다.
내용에 잘못된 부분이 있다면 댓글로 지적 부탁드립니다. 감사합니다.
'AI > Computer Vision' 카테고리의 다른 글
| [CS5670] Lecture 13: Stereo (0) | 2022.08.10 |
|---|---|
| [보충] Camera model and Vanishing points (0) | 2022.08.09 |
| [CS5670] Lecture 11: Panoramas (0) | 2022.08.08 |
| [CS5670] Lecture 10: Cameras (2) (0) | 2022.07.18 |
| [CS5670] Lecture 10: Cameras (1) pinhole, lens camera (0) | 2022.07.18 |




댓글