티스토리 뷰
Aliasing
출처: 위키디피아
Aliasing(앨리어싱)이란 무엇일까? 엘리어싱이란 위신호 현상의 의미로 신호 처리에서 표본화(샘플링)을 하는 가운데 각기 다른 신호를 구별해내지 못하게 하는 효과를 의미합니다.
신호가 샘플로부터 다시 구성될 때, 결과가 원래의 연속적인 신호와 달라지는 '일그러짐'을 가리키고, 계단 현상이라 부르기도 합니다.

- 붉은색 선: 실제 신호
- 검은색 실선: 샘플링 된 값
실제 신호보다 샘플링 된 값의 주기가 더 낮습니다. 이런 경우 sampling rate가 낮다고 하며, 신호를 제대로 해석할 수 없습니다. 이런 상황을 Aliasing이라고 합니다.
헷갈리는 몇 가지 용어를 정리해보자면
- Sampling: 무한한 continuous한 데이터들에서 유한한 데이터를 얻어내는 과정을 의미
- 현실 세계의 정보를 그대로 반영하면 continuous한 데이터가 추출됩니다. 이 결과는 의미 있는 정보를 제공해주지 않습니다. continuous한 데이터를 compact한 방법으로 바꿔줄 필요가 있으며, sampling이 그 과정입니다. 기본적으로 무한한 continuous data에서 유한한 data를 얻어내는 과정입니다.
- 수학적 개념에서 sampling은 모집단 전체의 수많은 데이터와 정보를 다 사용하면 비효율적이기 때문에 최소한의 의미 있는 정보를 사용하기 위해, 적당한 수의 데이터를 뽑아서 전체 모집단의 성질이나 패턴을 추정하기 위한 행동입니다. 이 의미가 이미지 관점에서도 데이터가 2차원으로 늘어났을 뿐, 의미는 크게 다르지 않습니다.
- Sampling rate: 이산적인 신호를 만들기 위해 연속적 신호에서 얻어진 단위 시간당 sampling 횟수

- Downsampling: sampling rate를 올리는 interpolation의 반대 개념. sampling rate를 변환하는 것
- Decimation: aliasing 왜곡을 완화시키는데 사용하는 필터 (aliasing은 신호의 sampling rate를 낮출 때 발생한다.)
Why aliasing occurs
앨리어싱은 신호의 변화를 포착하기에 불충분한 속도로 신호가 이산적으로 샘플링될 때 발생합니다.
신호가 이산적으로 샘플링되는 경우
- 망막 이미지(retinal image)는 광수용체(photoreceptors)에 의해 공간에서 샘플링됩니다.
- 영화와 비디오는 개별 프레임으로 시간에 따라 샘플링됩니다.
- 사운드는 일반적으로 녹음 및 통신을 위해 디지털 방식으로 샘플링됩니다.
sampling이 부적절하게 수행되면 이러한 모든 상황에서 앨리어싱이 발생할 수 있습니다. 앨리어싱이 발생하는 이유를 이해하는 것이 중요합니다.
Aliasing 발생 원인을 다시 정리해보자면
sampling rate가 이미지의 detail을 캡처할만큼 충분히 높지 않을 때 발생하고, 잘못된 신호로 이미지에 왜곡이 생깁니다. sampling rate는 이미지에서 가장 높은 frequency를 캡처할 수 있을만큼 충분히 높아야 합니다.
앨리어싱이 발생하는 이유를 살펴보았고, 뒤에는 이의 근거가 되는 Nyquist sampling theorem와 앨리어싱의 결과, 방지 방법까지 살펴보겠습니다.
- 발생 이유 - Nyquist sampling theorem에 근거하여
- 결과 - The wagon wheel effect
- 방지 방법 - Antialiasing
Nyquist sampling theorem
Nyquist sampling theorem은 sampling frequency는 적어도 신호에 포함된 가장 높은 frequency의 최소 2배여야 한다는 이론입니다.
식으로는 아래와 같습니다.
fs≥2fc
- fs: sampling frequency
- fc: highest frequency (contained in the signal)
예시로 살펴보겠습니다.
A single sinewave
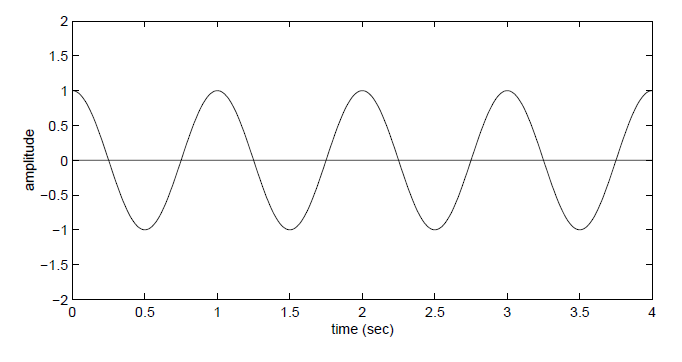
1 Hz의 frequency를 가집니다.
1. Sufficient to capture each peak and through of the signal

2. more than enough samples to capture the variations in the signal

3. not enough samples to capture all the peaks and throughs un the signal

이렇게 3가지의 예시를 살펴보았습니다.
처음의 signal이 1 Hz를 가지는 sinewave였습니다. 그러면 Nyquist sampling theorem의
fs≥2fc
해당 식에 따르면 aliasing이 발생하지 않기 위해선
fs≥2∗1Hz
로 최소 2 Hz 이상의 frequency를 가져야 합니다.
그럼 fig4~6을 순서대로 보면, 첫 번째 경우는 2 Hz로 충분한 경우에 해당합니다. 두 번째는 3 Hz으로 신호에서 변화를 감지하기에 충분한 sample이 존재합니다. 마지막은 1.5로 최소 2 Hz를 만족하지 못합니다.
이 경우에 1) losing information, 2) the wrong information의 결과를 불러 일으킵니다. 해당 samples에 대한 정보를 알지 못한다면, 해당 samples를 잘못 이해할 수 있습니다.
위의 예시를 통해 aliasing이 되는 원인을 살펴볼 수 있었습니다. 즉, 신호는 충분히 샘플링 되지 못할 때 aliasing이 발생합니다.
이제 더 복잡한 frequency components로 구성된 신호의 샘플링의 경우를 보겠습니다. Fourier's theorem에 따르면, 모든 continuous한 신호는 서로 다른 frequencies에서 sines과 cosines의 합으로 분해될 수 있습니다.

예를 들어 위의 waveform은 1Hz, 2Hz 및 3Hz의 frequencies에서 sinewaves를 더하여 구성되었습니다.

Nyquist sampling theorem에 따르면, fc=3이어서 fs=6이어야 합니다. 위의 경우는 충분한 samples를 갖고 있습니다.
따라서 신호에 하나가 아닌 여러 frequencies가 추가되면 앨리어싱을 방지하는데 필요한 최소 sampling rate는 다른 frequency components 수에 관계 없이 highest frequency의 두 배면 됩니다.
이제 aliasing이 발생했을 때 일어나는 현상을 살펴보겠습니다.
The wagon wheel effect
바퀴가 시계 방향으로 돌고 있음에도 불구하고 눈으로 볼 때 바퀴가 시계 반대 방향으로 도는 것처럼 보이는 효과를 의미합니다.
왜 이런 현상이 발생할까요?
영상에서 연속적으로 변화하는 이미지가 24fps의 속도로 이산적으로 샘플링됩니다.
시계 방향으로 초당 3회전(또는 180rpm)의 속도로 회전하는 8개의 spokes가 있는 수레 바퀴가 있다면, 수레 바퀴는 프레임당 하나의 spoke로 이동합니다.
이 경우에는 수레 바퀴가 정지해 있는 것처럼 보일 것입니다.
영상이 24fps를 갖고, 수레바퀴가 초당 3회전하는 8개의 spoke를 가졌기 때문에 1 spoke/frame으로 계산됩니다.
(3 revolutions/sec)∗(8 spokes/revolution)24 frames/sec=1 spoke/frame
다른 경우로 수레 바퀴가 이보다 약간 낮은 속도로, 예를 들어 초당 2.5회전한다면 이제 휠이 각 프레임의 spoke 간격의 83%만큼 이동하게 됩니다.

이러한 프레임을 빠르게 연속적으로 볼 때 직면하는 문제는 두 가지가 있습니다.
첫 번째는 휠이 시계 방향으로 spoke 간격의 83%만큼 움직였다는 것입니다.
두 번째는 spoke 간격의 17%만큼 이동했다는 것입니다.
눈은 두 번째를 받아들이게 됩니다. 그래서 결과적으로 바퀴가 뒤로 움직이는 것으로 감지하게 됩니다.
다시 쉽게 정리하자면, 바퀴 속도에 비해 프레임수가 적으면 반대로 가는 것처럼 보이는 효과를 의미합니다. 이는 영상에서 나타나는 앨리어싱의 예시입니다.

이제 마지막 접근입니다!
그렇다면 어떻게 앨리어싱을 막을 수 있을까요?
How to avoid aliasing
가장 쉬운 방법은 신호를 부드럽게 blurring을 해주는 것입니다.
blurring은 여러 인접한 픽셀의 값을 평균화하는 마스크로 필터링(또는 컨볼루션)하여 디지털 이미지에서 쉽게 수행할 수 있습니다.
blurring을 해주는 이유는 앨리어싱이 발생했을 때 이미지에서 나타나는 계단 현상 등을 줄일 수 있기 때문인 것 같습니다. (공부하며 더 정확히 알게 될 때 수정하겠습니다.)


blurring 방법으로 Gaussian filtering만 가볍게 보고 넘어가려고 합니다.
gaussian(가우시안 필터)는 mean filter와 다르게 단점을 보완합니다.
mean filter의 경우, 필터링 대상 위치에서 가까이 있는 픽셀과 멀리 있는 픽셀이 모두 같은 가중치를 사용하여 평균을 계산하여, 멀리 있는 픽셀의 영향을 많이 받게 됩니다.
하지만 가우시안 분포의 식을 사용하는 가우시안 필터는 가까운 픽셀은 큰 가중치를, 멀리 있는 픽셀은 작은 가중치를 사용하여 평균을 계산합니다.

blur → subsample → blur → subsample ... 입니다.
이 과정을 pyramid로 나타낼 수 있습니다.

왜 굳이 피라미드로 나타내었을까 생각해보았을 때, blurring하고 subsampling하는 과정을 시각화하기 위함 같습니다.
다시 본론으로 돌아가서 결국 앨리어싱을 줄이기 위한 솔루션으로 제안된 blurring을 보았는데요. 이는 이미지에 있는 maximum frequency를 효과적으로 줄이는 smoothing이라고 합니다.
즉, smoothing은 sub-sampling에서 놓칠 수 있는 빠른 변화를 제거합니다.
그래서 가우시안 피라미드를 쌓는 것은 두 가지 단계를 거치게 됩니다.
- Smoothing: 앨리어싱을 발생시키는 high frequency components를 줄입니다.
- Down-sampling(sub-sampling): 이미지를 각 1/2의 크기로 줄입니다.

subsampling은 마스크로 필터링하여 주변 픽셀 값을 이용하는 연산을 진행하는데요.
- How much space (number of pixels) does a Gaussian pyramid of an image take compared to the original image?
공부할 때 참고한 슬라이드엔 위와 같은 질문이 있는데요.
가우스 피라미드가 원본 이미지와 비교할 때 차지하는 픽셀 수는 얼마인지에 대한 질문입니다.
subsampling(=downsampling) 개념 자체가 이미지의 픽셀 수를 줄이는 과정이기 때문에, blurring과 subsampling을 하는 gaussian pyramid의 픽셀 수는 이미지 원본과 비교해봤을 때 당연히 줄어드는 것이라 생각합니다.
여기까지 aliasing을 주제로 발생 원인, 결과, 방지 방법 등을 크게 정리해보았습니다. 내용에 잘못된 부분이 있다면 지적 부탁드립니다.
Reference
[1] CSC320L10
[2] graphics, standford, courses, sampling
'AI > Computer Vision' 카테고리의 다른 글
| [CS5670] Lecture 6: Feature Descriptors and Feature Matching (0) | 2022.06.23 |
|---|---|
| [CS5670] Lecture 5: Feature Invariance (0) | 2022.06.23 |
| [CS5670] Lecture 4: Local features & Harris corner detection (0) | 2022.05.23 |
| [CS5670] Lecture 3: Image Resampling & Interpolation (0) | 2022.05.23 |
| [CS5670] Lecture 2: Edge detection (0) | 2022.05.19 |
- Total
- Today
- Yesterday
- style transfer
- 리눅스 나노
- 프롬프트
- 도커 컨테이너
- 파이썬 클래스 다형성
- docker
- support set
- 퓨샷러닝
- linux nano
- Prompt
- 구글드라이브연동
- NLP
- Unsupervised learning
- 파이썬 딕셔너리
- 딥러닝
- 리눅스 nano
- 서버구글드라이브연동
- 리눅스
- 도커 작업
- few-shot learning
- 파이썬
- 도커
- 파이썬 클래스 계층 구조
- clip
- python
- 리눅스 나노 사용
- cs231n
- prompt learning
- CNN
- stylegan
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |

