티스토리 뷰
뉴런의 내부 구조
- 가중치, 편향, 활성화 함수
- 입력값이 뉴런으로 전달되면, 각 뉴런마다 각각의 가중치(weight)와 곱해집니다.
- 편향(bias)이란 하나의 뉴런으로 입력된 모든 값을 다 더한 다음에(가중합, weighted sum) 이 값에 더해주는 상수입니다. 이 값은 하나의 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절합니다.
- 하나의 뉴런에서 다른 뉴런으로 신호를 전달할 때 어떤 임계점을 경계로 출력값이 큰 변화가 있는 것으로 추정합니다.
- 출력값에 변화를 주는 함수를 이용하는데 이게 활성화 함수입니다.
- 편향이 임계점을 얼마나 쉽게 넘을지 말지를 조절해줍니다.
- DNN은 데이터를 입력받아 그 데이터들에 대한 각기 다른 가중치를 곱해 다음 층의 뉴런으로 전달하는 과정을 반복적으로 거치며 마지막에 최종적으로 출력값을 계산합니다.
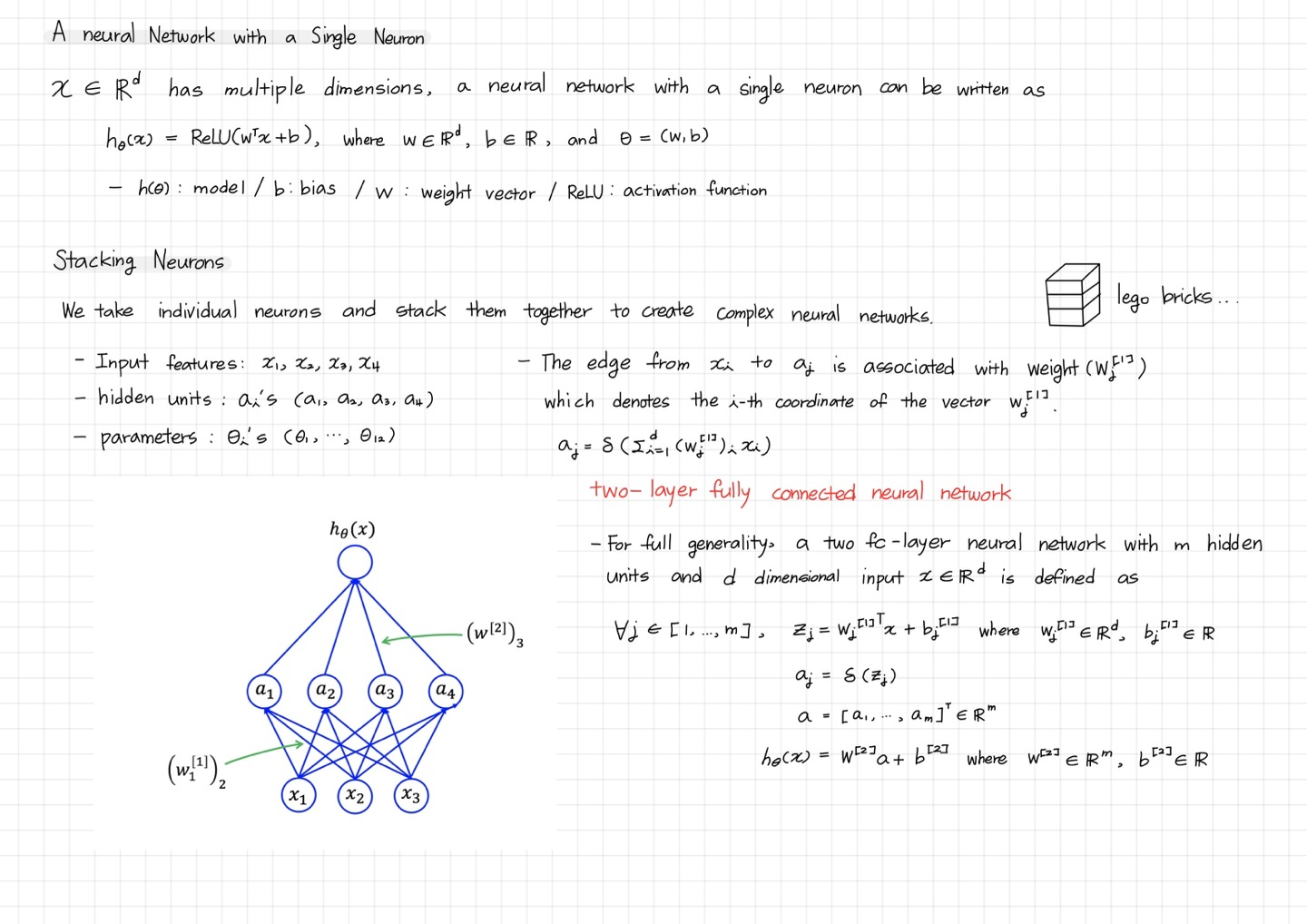
A neural network with a single neural
Stacking Neurons
Vectorization
Connection to the kernel method

학습 가능한 매개변수의 수
- Input layer: 모든 input layer는 입력 이미지를 읽으므로 여기서는 파라미터가 없습니다. → 0개
- Convolution layer: Conv layer는 $l$개의 feature maps을 갖고, k개의 출력 feature maps을 갖습니다. 그리고 filter의 사이즈는 $n$x$m$입니다.

- 위 이미지로 예시를 들면, $l=32$, $k=64$, $n=3$, $m=3$입니다. 그러면 결국 $3*3*32$의 filter가 있다고 이해해야 합니다. 그리고 64개의 서로 다른 $3*3*32$의 filter를 학습합니다.
- 따라서 가중치의 총 개수는 $n*m*k*l$이며, 각 feature map에 대한 bias term도 있으므로 총 파라미터 수는 $(n*m*l+1)*k$입니다. → $(n*m*l+1)*k$
- Pooling layer: pooling layer는 2x2(e.g)의 이웃에서 최댓값을 취하는 방식으로 파라미터가 없습니다. → 0개
- Fully-Connected layer: 모든 입력 뉴런은 각 출력 뉴런마다의 가중치를 갖고 있습니다. $n$개의 inputs, $m$개의 outputs이 있을 때, 필요한 가중치의 수는 $n*m$이며, 각 출력 뉴런마다 bias를 더해준다면 $(n+1)*m$입니다. → $(n+1)*m$
- Output layer: output layer는 일반적인 FC-layer이므로 $(n+1)*m$ 파라미터이고, $n$은 입력 수, $m$은 촐력 수입니다.
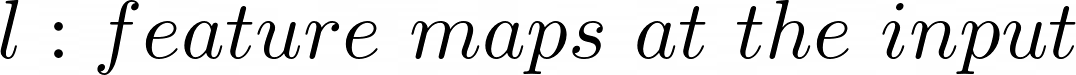
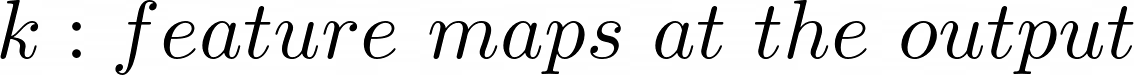


Convolutional filters
- 컨볼루션 필터는 해당 필터 내에서 학습된 가중치를 기반으로 feature map을 구성합니다.
- 일부 필터는 edge, textures를 학습하며 집합적으로 input image에 있는 class 정보의 다양한 feature representations을 학습합니다.
- 따라서 채널 수는 입력의 다양한 feature map을 학습하는 filter의 수를 나타냅니다.
- 또한, feature map은 중요도가 다릅니다.
- 예를 들어, edge 정보를 포함하고 있는 feature map이 배경의 texture transition을 학습하는 다른 feature map에 비해 더 중요할 수 있습니다.
- counterpart feature maps에 비해 더 높은 중요도를 가진 더 중요한 feature maps을 원합니다.
Channel Attention
- 이 개념이 "channel attention"의 기초가 되며, 기본적으로 다른 채널보다 특정 채널이 더 높은 중요성을 부여하는 더 중요한 채널에 "attention"을 집중하려고 합니다.
- 그 관점에서 Squeeze-Excitation Networks의 논문이 제안되었습니다.
- 압축시키는 것이 더 효과가 있었던 이유?
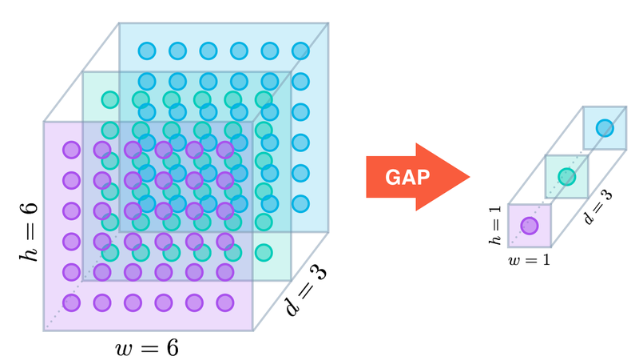
- SqueezeNet에서는 채널 방향으로 GAP(global average pooling)을 적용하여서, 압축된 정보를 활용하여 중요한 채널이 활성화되도록 하였습니다.
- 채널 관점에서의 중요한 정보를 뽑아내서 channel-wise feature dependency를 통해 성능을 올릴 수 있었습니다.
- 그리고 Excitation operation과정에서 channel dependency에 근거하여 self-gating mechanism을 적용합니다. 즉, 앞서 말했다시피 필요한 channel들에 대해서는 좀 더 부각해주고 그렇지 않은 channel들은 버리는 과정을 거치게 됩니다.
- 이 SE Block을 반복적으로 쌓으면서 중요한 feature를 계속해서 추출하게끔 합니다.
Squeeze and Excitation
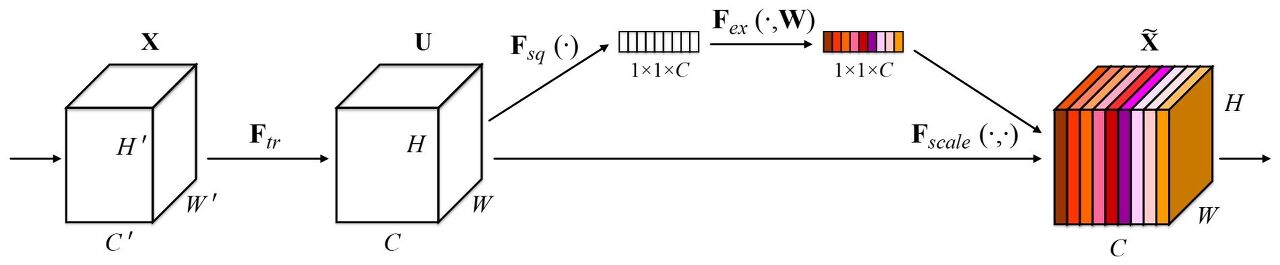
- Squeeze: a global average pooling operation
- Excitation: two small FC layers
― 각 SE block은 squeeze 단계에서 GAP, excitation 단계에서는 2개의 작은 FC layer와 그 뒤에는 비용이 저렴한 channel-wise scaling이 수행됩니다.

GAP와 bottleneck FC layer 간의 parameter와 두 FC layer 간의 parameter를 계산하면 아래와 같습니다.

- 입력의 형태 $(c*1*1)$이고, input layer엔 $C$만큼의 뉴런 수가 존재합니다.
- 은닉층은 reduction ratio $r$만큼 감소 시켜 총 $\frac{C}{r}$의 뉴런 수를 갖게 됩니다.
- 출력은 입력과 동일한 차원 공간으로 다시 투영되어 총 $C$ 뉴런으로 돌아갑니다.
input channel, out channel, filter size가 곱해져 $C^2$이 나오고, 두 번의 FC-layer가 존재하기 때문에 2를 곱하고, $r$은 reduction ratio에 해당합니다.
추가로 논문을 읽으며 생각 해본 것
1. Trade-off between improved performance and increased model complexity
성능과 모델의 복잡도는 trade-off를 가지고 있습니다. 하지만 모델의 복잡도를 제한하면서 더 좋은 일반화를 돕기 위해, 2개의 FC-layer를 통해 non-linearity를 증가시켰습니다. 또한 bottleneck 구조를 통해 dimensionality-reduction layer 역할을 하도록 만듭니다.
2. GAP(Glogal average pooling) and GMP(Global max pooling)

― 실험 결과에서는 GAP가 더 좋게 결과가 나왔습니다. 그 이유는?
― Max pooling은 pixel의 가장 큰 활성화 값을 유지시킵니다. 그 이웃의 픽셀과 noisy한 값은 고려하지 않습니다.
― 반대로 Average pooling의 경우, 특정 픽셀 정보를 그대로 유지시키진 않지만, 윈도우 크기만큼의 픽셀 정보를 평균내어 더 smoother하게 구성합니다.
― (GAP는 feature map의 모든 픽셀 정보를 평균내서 하나의 sigular value로 줄입니다. 입력값 $(C*H*W)$를 $(C*1*1)$로 줄이며, 본질적으로 이것은 길이가 $C$인 vector입니다. 여기서 각 feature map은 이제 singular value로 분해되는 것입니다.)
3. ReLU, Tanh, Sigmoid
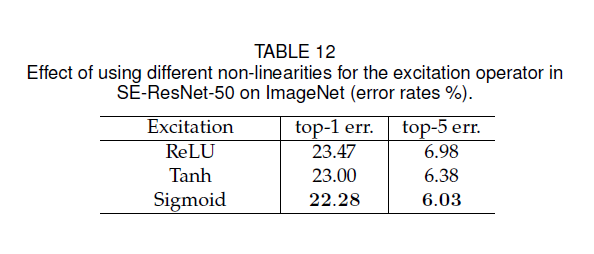
[0, 1] 범위로 조정하는 Sigmoid activation layer를 통과해서 결과적으로 출력은 Excitation module의 MLP에서 학습된 해당 가중치로 입력 텐서의 각 channel, feature map을 확장하는 간단한 element-wise multiplication로 적용됩니다. 각 채널의 중요도를 0과 1 사이의 값으로 파악할 수 있게 해주고, 마지막으로 U에 곱해져 재보정하여 최종적인 feature를 추출합니다.
즉, Sigmoid가 더 성능이 좋고 선택한 이유는 Squeeze에서 얻은 요약된 정보를 사용하기 위해, 채널 간의 비선형성을 학습할 수 있어야 하면서 여러 채널을 강조할 수 있도록 상호 배타적인 관계를 학습할 수 있기 때문입니다.
→ 가장 중요한 하나의 채널만 활성화 시키는 것이 아닌 여러 채널들이 서로 다른 정도로 활성화되기로 하기 위한 목적
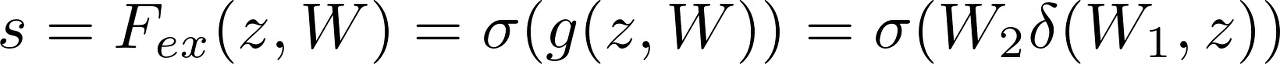
데이터셋에 정답 라벨이 하나뿐인 단순 분류 모델 활성화 함수로 소프트맥스(SoftMax)를 사용해서 단 하나의 최댓값을 찾지만, 하나의 대상에도 여러 개의 클래스의 정답 라벨을 지정할 수 있는 다중 라벨 분류(multi label classification)에서는 시그모이드를 사용하는 것과 같은 방식으로 이해했습니다.
이렇게 계산된 벡터를 기존의 특성 맵에 채널에 따라서 곱해주어 중요한 채널이 활성화 되도록 만들어 줍니다.
'AI > Deep Learning' 카테고리의 다른 글
| Siamese Networks for Pairwise Similarity (0) | 2022.11.25 |
|---|---|
| Few-shot learning 기본 개념(Basic concepts) (0) | 2022.11.25 |
| Meta learning, training 과정, bi-level optimization (0) | 2022.11.16 |
| Autoencoder란? - PyTorch로 구현하기 (0) | 2022.11.08 |
| C4W2L03-04 Resnets & Why ResNets Work (0) | 2022.11.06 |
- Total
- Today
- Yesterday
- 파이썬 클래스 계층 구조
- 리눅스 나노
- 서버구글드라이브연동
- 리눅스 나노 사용
- python
- prompt learning
- stylegan
- 파이썬 딕셔너리
- 딥러닝
- linux nano
- support set
- style transfer
- 도커
- docker
- 파이썬 클래스 다형성
- 파이썬
- NLP
- Prompt
- CNN
- clip
- 퓨샷러닝
- 리눅스 nano
- 구글드라이브연동
- 프롬프트
- 도커 작업
- 도커 컨테이너
- Unsupervised learning
- few-shot learning
- cs231n
- 리눅스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

