티스토리 뷰

2016년 ECCV에서 게제된 논문 Deep Networks with Stochastic Depth 입니다.
Abstract
현재까지 benchmark에서 error를 낮췄던 것은 Very Deep Convolution Network입니다. 이렇게 깊은 네트워크를 가진 경우 몇 가지 문제점이 있습니다. gradient vanishing 문제로 forward flow에서 감소하며, training time이 느려질 수 있습니다.
해당 문제를 해결하기 위해 Stochastic Depth를 제안합니다. 이는 train time에 short network를 훈련하고, test time에 deep network를 사용하는 모순되어 보이는 방법입니다. 또한, 각 mini-batch에 대해 계층의 하위 집합을 무작위로 drop하고, identity function으로 bypass합니다.
이 간단한 접근 방식이 최근의 (논문 기준) residual network를 보완하였고, 훈련 시간을 줄이며 test error를 개선합니다.
Introduction
Vanishing Gradients
gradient information이 back-propagated 됨에 따라 multiplication과 convolution이 반복되는데 여기서 이전 layer에서 넘어오는gradient 정보들이 비효율적으로 작게 만듭니다. 이를 해결하기 위해 careful initialization, hidden layer superision, Batch Normalization 등의 접근 방식이 존재합니다.
Diminishing feature reuse
loss in information flow라고도 합니다. 즉, forward propagation 동안 feature를 재사용하는 것이 줄어드는 문제로 기울기가 사라지는 것과 유사한 문제입니다.
해당 문제도 input instance의 feature 또는 이전 레이어에서 계산된 feature들이 multiplication과 convolution이 반복되며 wash out(세척)되어 의미 있는 gradient direction을 식별하고 학습하기 어렵게 만든다는 점입니다.
따라서 최근의 새로운 아키텍처들은 레이어 간의 직접 identity mapping을 통해 이 문제를 우회하려고 합니다. 이를 통해 네트워크는 이전 레이어의 방해 없이 feature를 전달할 수 있습니다.
Long training time
네트워크가 깊어질수록 커지는 문제입니다. forward와 backward 할 때 네트워크의 깊이는 계속 커집니다.
네트워크가 짧을수록 information flow는 forward와 backwrad시 이점을 갖고, 합리적인 시간 내에 효과적으로 학습합니다. 하지만 컴퓨터 비전에서 흔히 볼 수 있는 복잡한 개념을 표현할 만큼 표현력이 부족합니다. 깊은 네트워크는 모델 복잡성이 훨씬 더 크지만, 실제로 훈련하기 어렵고 많은 시간이 걸립니다.
이런 고유한 딜레마로 인해 deep networks with stochastic depth를 제안하였으며, 해당 알고리즘은 겉보기엔 대조적인 인사이트에 기반합니다.
deep network during testing but a short network during training
Idea Approach
― Residual Network architecture로 해결
― small expected depth during training
― 각 샘플 또는 미니배치에 대해 상당한 부분의 layer를 randomly하게 제거하여 network를 단축
― a large depth during testing
Results
― 1) training time, 2) test error가 줄어듦
이런 결과가 나타난 것의 요인을 살펴보면
1) 짧은 forward, backward에 기인하므로 전체 깊이로 확장되지 않고, 네트워크의 expected depth가 짧아집니다.
2) depth가 줄어들면 forward propagation 단계와 gradient computation의 chain이 감소하여서, 특히 backward propagation 동안 이전 레이어에서 gradient를 강화합니다.
또한, stochastic depth로 훈련된 네트워크는 implicit ensemble로 볼 수 있습니다. (network에 대해 다른 depth의 네트워크를 사용하는)
요약
― VGGNet 논문 등에서 CNN의 layer가 깊어질수록 성능이 좋아진다는 것을 확인
― 하지만 깊어질수록 gradient vanishing/exploding 같은 문제
― 해결하기 위해 weight initialization, Batch Normalization 방법 적용
― ResNet은 Residual Learning을 통해 Degradation problem 문제 해결
― 그러나 학습 시간이 너무 오래 걸리고, gradient vanishing 문제도 여전히 존재
― layer를 무작위로 drop하고 identity function으로 circumvent(우회)하는 방법 제시 → Stochastic Depth
Background
Residual netwokrs(ResNets)
네트워크가 깊어질수록 gradient와 training signal이 많은 레이어를 통해 전파될 때 사라지기 때문에 function approximation에서 더 나빠질 것이라 생각했습니다.
수정 사항으로 네트워크에 skip connections를 추가할 것을 제안합니다.
Hl이 l번째 레이어의 출력을 나타내고, fl(·)는 레이어가 l−1에서 l로의 일반적인 convolution transformation을 나타냅니다. id(·)는 identity transformation을 나타내며 ReLU transition function을 가정합니다.


Dropout

― Dropout: make the network thinner
― Stochastic depth: make the network thinner and shorter
드롭아웃은 임의의 확률 p로 node를 일부만 선택하는 방법입니다. 단점으로는 모델이 깊어지면 regularize 기능을 잃어버리고, BatchNorm은 Dropout과 같이 사용하면 효과를 잃습니다. Dropout은 Batch Normalization이 있는 100-layers ResNet에서 사용할 때 개선되지 않았습니다.
이러한 이전 접근 방식을 기반으로 Stochastic depth를 제안하였습니다. 이는 Block을 아예 건너뛰는 방법입니다.
Deep Networks with Stochastic Depth
ResNet architecture

fl: Conv - BN - ReLU - Conv - BN
Stochastic depth
training 동안 네트워크의 깊이를 줄이는 동시에 tesing에는 변경되지 않게 하는 것이 목표입니다.
training 중 ResBlock을 무작위로 삭제하고 skip connection을 통해 할 수 있는데, 이를 Bernoulli random variable에 따라 active 또는 inactive를 결정합니다. (b∈0,1) 또한, ResBlock의 active probability를 p=Pr(b=1)로 표시합니다.
이 정의를 통해 fl에 bl을 곱하여 lth의 ResBlock을 우회할 수 있으며, 업데이트 규칙을 식 (2)로 확장시킵니다.

― bl=1이면 original ResNet (1)로 축소
― bl=0이면 ResBlock은 identity function으로 축소 → (3)

이 stochastic depth에서 식 Hl−1 은 무조건 non-negative임을 따라야 합니다. 물론 activation function을 relu로 사용하기 떄문에 non-negative하지만, 첫 번째 레이어일 경우를 고려해야 해서 l≥2여야 합니다. l=1에선 input이 Conv-BN-ReLU의 output을 가집니다.
The survival probabilities
pl은 새로운 하이퍼 파라미터이고, ResBolocks과 이웃한 근처 값을 가져야 합니다. 여기서 최적의 확률 p가 무엇인지 찾아야 합니다.
한 가지 옵션으로 하이퍼 파라미터를 얻기 위해 모든 pl=pL을 일률적으로 전부 설정하는 방법이 있습니다. 다른 가정은 l의 smooth function을 통해 정하는 방법이고, 식은 아래 (4)와 같습니다.
단순한 linear decay rule을 따르며, p0=1에서 마지막 레이어인 pL까지 시행합니다.
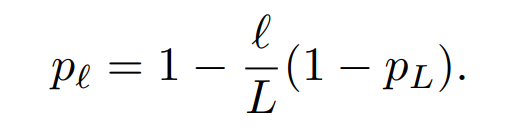
1. Uniform
2. Linear decay → (4)

Fig 2를 보면, 초기 레이어가 더 나중의 레이어보다 더 낮은 low-level feature를 추출하므로 더 안정적으로 존재해야한다는 것에서 비롯되며, pL이 0.5일 때 가장 안정적임을 확인하고 0.5로 설정합니다.

― Stochastic Depth (linear decay)
- - - Stochastic Depth (uniform)
- - - Constant Depth
Expected network depth
transformation fl는 (1−pl)의 확률로 bypass하며 깊이가 감소됩니다.
stochastic depth에 대해 training 시 ˜L은 random variavle이 되고, 이 effective ResBlock 수는 ˜L의 기댓값으로 E(˜L)=ΣLl=1pl로 주어집니다.
이때 pL=0.5이고 L이 크면 E(˜L)=3L/4로 수렴합니다.
연결이 무작위이기 때문에 훨씬 더 짧아진 네트워크와 개별 layer에 대한 더 직접적인 경로 업데이트가 있습니다. 아래에 설명이 이어집니다.
Training time saving
ResBlock을 bypass하는 방법은 특정 반복에 대해서 forward-backward computation 또는 gradient updates가 필요 없습니다.
네트워크의 깊이가 줄어들었으니 training time이 당연히 줄어들었고, pL=0.5의 linear decay rule을 따르니 25%의 시간이 절약되었습니다.
Implicit model ensemble
stochastic depth를 사용한 training이 ResNet의 ensemble을 implicitly 훈련하는 것을 알 수 있습니다.
L개의 각 레이어는 active or inactive 상태이므로 2L 네트워크 중 하나가 샘플링 되고 업데이트됩니다. 테스트하는 동안 다음 단락의 접근 방식을 사용하여 모든 네트워크의 평균을 구합니다.
Stochastic depth during testing
테스트할 때는 약간의 수정이 필요합니다.
전체 모델 용량으로 전체 네트워크를 활용하기 위해서 테스트 전체에 걸쳐 모든 fl을 active한 상태로 유지합니다. 그러나 training 시엔 업데이트의 일부에서만 활성화되었고 다음 레이어틔 해당 가중치가 pl에 보정되었습니다.
따라서 test 시에도 예상 pl만큼 보정해야 합니다.

위 식은 가능한 모든 네트워크를 단일하게 결합하는 형태로 해석될 수 있으며, 여기서 각 레이어는 survival probability에 따라 가중치가 부여됩니다.
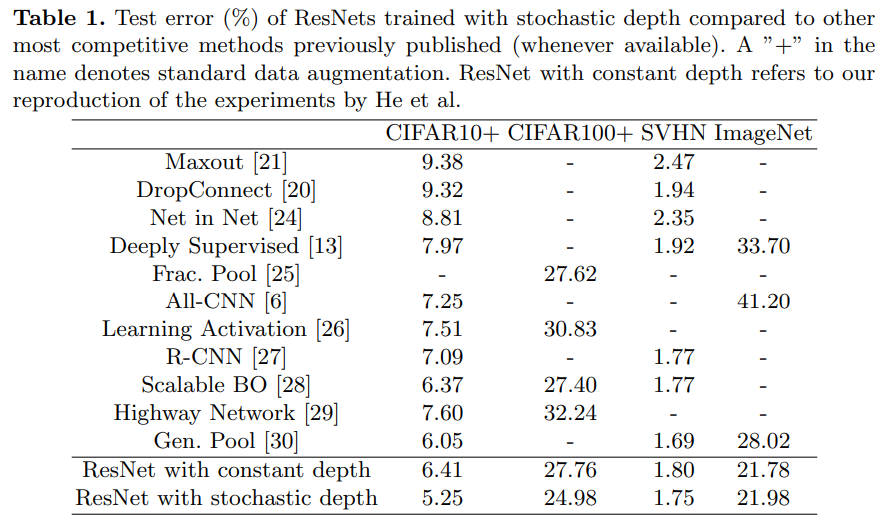
Results
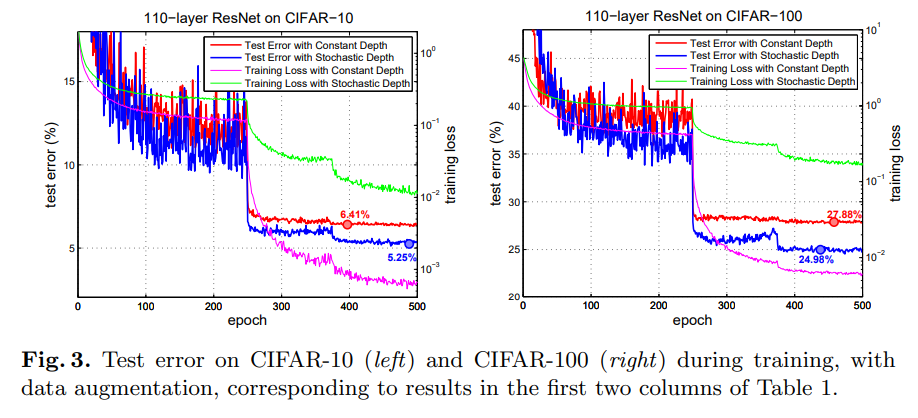

gradient의 평균 절대값을 보여줍니다. 수직으로 표시된 점선은 learning rate의 분할을 의미합니다. (learning rate by a factor of 10, which cause gradients to shrink)
learning rate가 떨어진 후의 gradient의 크기는 크게 작아지는데요. 이는 gradient vanishing의 문제의 관점에서 살펴보면 Stochastic Depth의 네트워크가 더 효과적으로 훈련한다는 점을 뒷받침하기도 합니다.
gradient가 크게 떨어지는 것과 안정적으로 유지되는 것으로 비교할 수 있습니다.



Conclosion
― test 시 전체 깊이를 유지하면서 훈련 동안 네트워크의 깊이를 줄이는 방법: Stochastic Depth
― training time을 줄입니다.
― 네트워크의 깊이를 1,000개 레이어 이상으로 늘릴 수 있으며 test error를 줄입니다.
'Review > Paper' 카테고리의 다른 글
| [논문 리뷰] Attention Is All You Need (0) | 2023.01.04 |
|---|---|
| [논문 리뷰] Neural Machine Translation by jointly Learning to Align and Translate (0) | 2023.01.02 |
| [논문 리뷰] Automatic Data Augmentation for Generalization in Reinforcement Learning (0) | 2022.12.16 |
| [논문 리뷰] Batch Normalization: 논문으로 공부하고 이해하기 (0) | 2022.10.17 |
| [논문 리뷰] PSPNet(Pyramid Scene Parsing Network) (2) | 2022.07.31 |
- Total
- Today
- Yesterday
- style transfer
- 딥러닝
- prompt learning
- Unsupervised learning
- 리눅스
- python
- docker
- 파이썬
- 도커 작업
- 파이썬 클래스 계층 구조
- cs231n
- 리눅스 나노 사용
- 퓨샷러닝
- 프롬프트
- 도커 컨테이너
- 파이썬 클래스 다형성
- 파이썬 딕셔너리
- 도커
- 리눅스 나노
- 구글드라이브연동
- stylegan
- few-shot learning
- 리눅스 nano
- NLP
- 서버구글드라이브연동
- linux nano
- support set
- CNN
- clip
- Prompt
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

