티스토리 뷰
[논문 리뷰] Neural Machine Translation by jointly Learning to Align and Translate
Suyeon Cha 2023. 1. 2. 18:35참고 출처
- [Paper Review] Neural Machine Translation by Jointly Learning to Align and Translate
- 15. 어텐션 메커니즘 (Attention Mechanism)
- [NLP | 논문리뷰] NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
- 딥러닝 논문 리뷰 >> NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE 리뷰
해당 논문을 읽고, 위의 유튜브 리뷰 영상과 블로그 정리 글을 통해 필요한 부분만 정리했음을 밝힙니다. 또한, 아키텍처의 구조는 김탁영님의 자료를 첨부하였음을 밝힙니다. 감사합니다.

해당 논문은 'Neural Machine Translation by jointly Learning to Align and Translate'의 제목으로 2016년에 ICLR에서 발표된 논문입니다. 흔히들 attention이라 부르는 논문이며, 저자의 이름을 따서 Bahdanau attention이라고 부릅니다.

(2016년 기준) 최근 기계 번역으로 Neural machine translation이 제안되었습니다. 단일 뉴럴 네트워크를 쌓아서 번역 성능을 올리고자 했습니다. 해당 모델은 encoder와 decoder로 쌍을 이루는 구조를 가졌는데, 입력 문장을 고정된 길이의 벡터로 encoding하고, decoder는 해당 벡터를 이용해서 번역된 결과를 생성해냅니다.
이러한 encoder-decoder 구조는 bottleneck 문제를 발생시킬 수 있었습니다. 원인으로는 인코더가 억지로 전체 문장을 하나의 고정된 길이의 벡터로 생성하고자 할 때였으며, 문장이 길어질수록 더 심하게 나타납니다. 논문에서는 30 단어가 넘게 되면 성능이 급격하게 저하되는 것을 발견할 수 있었습니다.
결과적으로 해당 논문은 입력으로 들어오는 문장에 대해서 강건하고, 통계적 계산에서 벗어나는 모델로 여기서 encoder와 decoder를 다르게 설계하여 성능을 올리고자 했습니다.
이 논문에서는 기본적인 RNN Encoder-Decoder 구조에 대한 설명, 그 다음에 논문에서 설계한 구조 Align and Translate를 설명하기 위해, Decoder(General Description), Encoder(Bidirectional RNN for Annotation Sequences)를 순서대로 설명합니다.
Encoder

BiRNN입니다. forward, backward 두 개의 RNN으로 구성되며, forward RNN은 순차적으로 읽어 hidden state를 생성하고, backward는 역방향으로 읽어서 역방향의 hidden state를 생성합니다.
같은 시각 j에서 입력 $x_j$에 대해서 forward, backward hidden state를 연결해서 j번째 hidden state를 생성합니다.
이러한 구조적 특징으로 인접한 state의 정보를 더 많이 갖게 됩니다.

Decoder
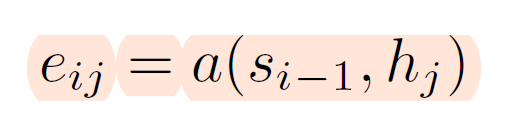
decoder에서 hidden state도 존재합니다. 시각 i에서의 hidden state를 $s_i$라고 합니다. 그리고 $s_i$는 encoder의 각 시각 j에서의 정보와 얼마나 연관성이 있는지 score를 계산하게 됩니다. 이를 attention score라고 보면 되고, 논문에서는 alignment model이라 합니다.

position $j$ 주위의 input과 position $i$ 주위의 output 값이 얼마나 매치되는지의 점수를 계산합니다. 디코더의 은닉층과 인코더의 은닉층의 내적을 통해 스칼라 값으로 계산됩니다.
디코딩 할 때 어느 입력 시점에 더 집중할 것인지를 점수화한 것이고 디코딩의 시점 i에서 모든 입력 시점에 대해 계산이 되며 모든 디코딩 스텁에서 반복됩니다.
그 다음은 attention distribution입니다.
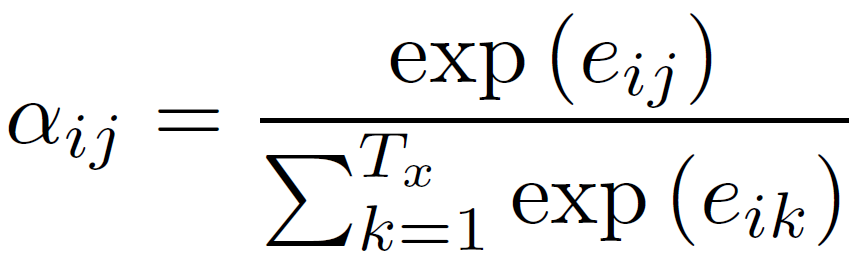
softmax 식입니다. attention score를 통해 softmax 함수를 통과 시켜 확률로 바꿉니다. 계산된 각 0~1 사이의 값들이 나중에 입력 시점에 대한 가중치 역할을 하게 됩니다. 얼마나 attention 할지를 결정시키는 값이라 볼 수 있습니다.
그 다음은 weighted sum 파트입니다.
인코더의 hidden state와 attention 가중치 값들을 곱하고 모두 더합니다.
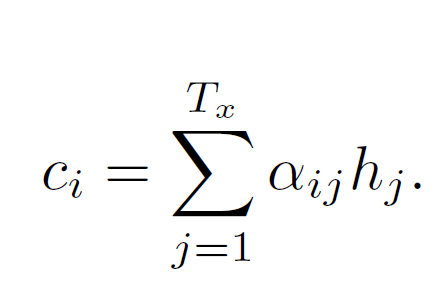
weighted sum을 하나의 context vector로 만들어서 decoder에 보내줍니다. 기존 모델은 encoder가 만든 잠재 변수를 그대로 사용하는 경우가 많았다면, 이렇게 가중치를 곱해줘서 각각의 output을 생성해서 모델의 성능을 올려줄 수 있게 된 것입니다.

기존의 인코더-디코더 접근 방식과 달리 여기서 확률은 각 대상 단어 $y_i$에 대해 별개의 context vector $c_i$에 따라 결정된다는 점에 유의해야 합니다.

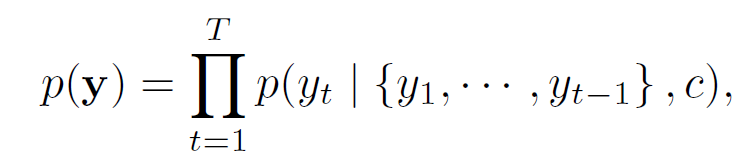
즉, 이전 방식과의 차이점은 fixed-length vector가 매 시간 인덱스마다 다르게 반영된다는 점입니다.
실험 결과와 성능은 생략하겠습니다.
결론적으로 고정된 크기의 벡터에 입력 정보를 모두 담아야 했던 기존의 방식에서 벗어나, 모델이 다음 target word를 생성하는 것과 관련 있는 정보에만 집중(attention)하도록 길이에 robust하게 만들었습니다.
정리
※ 참고자료 1번 유튜브 영상에서 가져온 자료입니다.
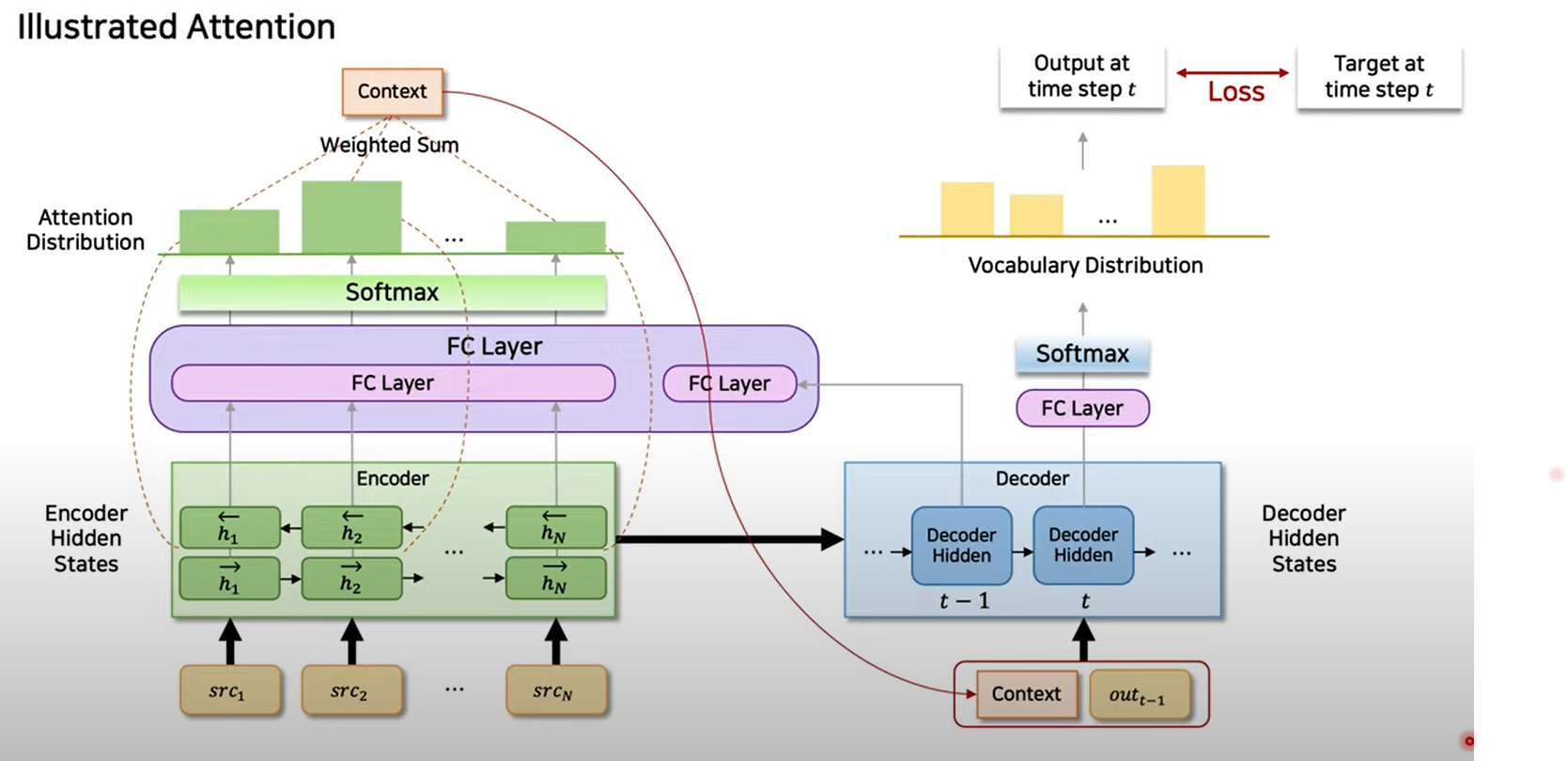
- source sequence가 RNN 기반의 Encoder에 들어오게 됩니다. Forward 방향으로 recurrent를 진행하기도 하고, backward 방향으로 진행할 수 있는데 이를 합쳐 Bidirectional 한 모델 BiRNN을 사용합니다.
- 일반적인 Encoder-Decoder 과정에 따라서 인코딩을 끝냈으므로 디코더로 넘어갑니다. $t-1$번째 시점까지의 hidden state를 구했다고 가정하고, $t$번째 hidden state를 구하기 위한 과정을 살펴봅니다.
- Decoder의 hidden state는 FC layer를 거치고, Encoder의 각 representation마다 FC layer를 거쳐 이 둘을 더해줍니다. 더한 후에 tan h를 적용하고, 한 번 더 FC layer를 거쳐 입력 시퀀스와 동일한 길이의 score를 산출해 냅니다.
- score를 산출하면 softmax를 거쳐 하나의 분포로 만들어 줍니다. 이 분포를 attention distribution이라고 합니다.
- 이 분포가 완성이 되었다면, Encoder의 시퀀스와 같은 길이이기 때문에 가중치로 작용하는 attention distribution을 hidden state와 곱해서 최종 representation을 얻기 위한 weighted sum을 진행하여, context vector를 얻습니다.

- 위에서 구한 context vector는 $t$ 시점의 hidden state를 구하기 위해 쭉 그대로 사용되고, $t-1$ 시점의 output과 concatenate를 통해서 $t$ 시점의 입력으로 들어가게 됩니다.
- 그러면 Decoder의 hidden state가 나오고 FC layer - Softmax를 거쳐 $t$ 시점의 output을 예측할 수 있게 됩니다.
- 그리고 $t$ 시점의 output과 $t$ 시점의 target 값의 차이를 통해 Loss를 구하여 학습을 진행합니다.
위키독스를 보고 그대로 복사하여 정리한 내용 (위에 출처 밝혀두었습니다.)
Attention Mechanism
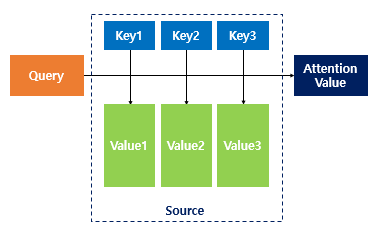
Attention(Q, K, V) = Attention Value
- 주어진 '쿼리(Query)'에 대해서 모든 '키(Key)'와의 유사도를 각각 구합니다.
Q = Query : t 시점의 디코더 셀에서의 은닉 상태 K = Keys : 모든 시점의 인코더 셀의 은닉 상태들 V = Values : 모든 시점의 인코더 셀의 은닉 상태들
1) 어텐션 스코어(Attention Score)를 구한다.
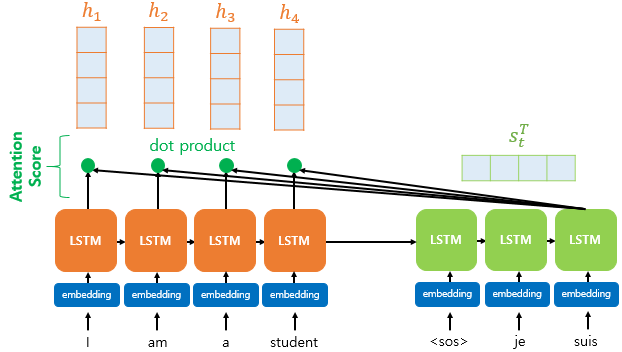
어텐션 스코어란?
현재 디코더의 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 $s_t$와 얼마나 유사한지를 판단하는 스코어값입니다.
닷-프로덕트 어텐션에서는 이 스코어 값을 구하기 위해 $s_t$를 전치(transpose)하고 각 은닉 상태와 내적(dot product)을 수행합니다. 즉, 모든 어텐션 스코어 값은 스칼라입니다. 예를 들어 $s_t$과 인코더의 $i$번째 은닉 상태의 어텐션 스코어의 계산 방법은 아래와 같습니다.
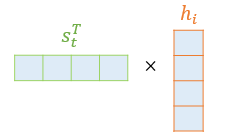
$score(s_t, h_i) = s_i^T h_i$
$s_t$와 인코더의 모든 은닉 상태의 어텐션 스코어의 모음값을 $e_t$라고 정의하겠습니다. $e_t$의 수식은 다음과 같습니다.
$e_t = [s_t^Th_1, \dots, s_t^T h_N]$
2) 소프트맥스(softmax) 함수를 통해 어텐션 분포(Attention Distribution)를 구한다.
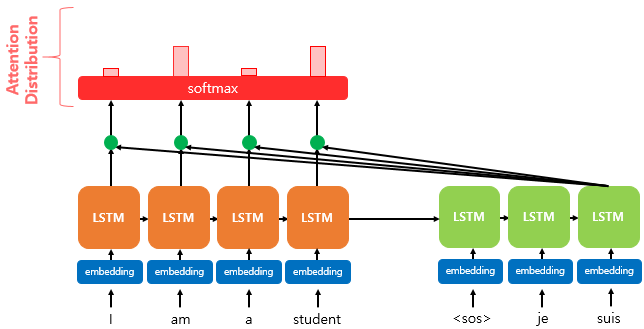
어텐션 분포(Attention Distribution)란?
$e^t$에 소프트맥스 함수를 적용하여, 모든 값을 합하면 1이 되는 확률 분포를 말합니다. 각각의 값은 어텐션 가중치(Attention Weight)라고 합니다.
디코더의 시점 $t$에서의 어텐션 가중치의 모음값인 어텐션 분포를 $α^t$이라고 할 때, $α^t$을 식으로 정의하면 다음과 같습니다.
$\alpha^T = \frac{exp(e_{ij})}{\Sigma^{T_x}{k=1}exp(e{ik})}$
3) 각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값(Attention Value)을 구한다.
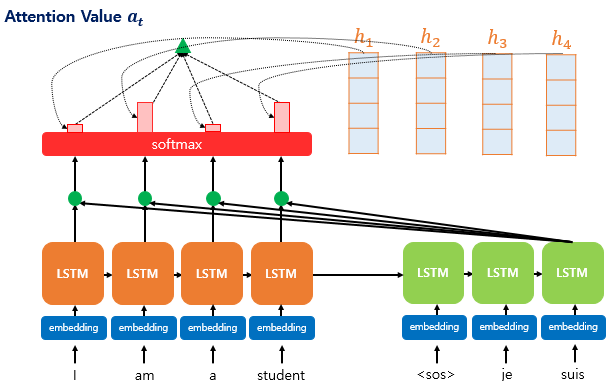
어텐션의 최종 결과값을 얻기 위해서 각 인코더의 은닉 상태와 어텐션 가중치값들을 곱하고, 최종적으로 모두 더합니다.
요약하면 가중합(Weighted Sum)을 진행합니다. 아래는 어텐션의 최종 결과. 즉, 어텐션 함수의 출력값인 어텐션 값(Attention Value) $a_t$에 대한 식을 보여줍니다.
$a_t = \Sigma^N_{i=1}a^t_i h_i$
이러한 어텐션 값 $a_t$은 종종 인코더의 문맥을 포함하고 있다고하여, **컨텍스트 벡터(context vector)**라고도 불립니다.
4) 어텐션 값과 디코더의 t 시점의 은닉 상태를 연결한다.(Concatenate)
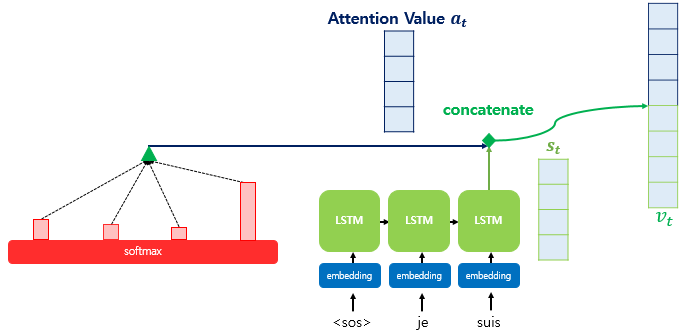
어텐션 함수의 최종값인 어텐션 값 $a_t$을 구했습니다. 사실 어텐션 값이 구해지면 어텐션 메커니즘은 $a_t$를 $s_t$와 결합(concatenate)하여 하나의 벡터로 만드는 작업을 수행합니다.
이를 $v_t$라고 정의해보겠습니다. 그리고 이 $v_t$를 $\hat{y}$ 예측 연산의 입력으로 사용하므로서 인코더로부터 얻은 정보를 활용하여 $\hat{y}$를 좀 더 잘 예측할 수 있게 됩니다. 이것이 어텐션 메커니즘의 핵심입니다.
5) 출력층 연산의 입력이 되는 $\hat{s_t}$를 계산합니다.
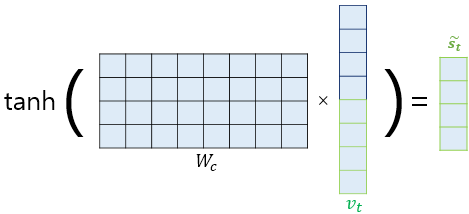
논문에서는 $v_t$를 바로 출력층으로 보내기 전에 신경망 연산을 한 번 더 추가하였습니다.
가중치 행렬과 곱한 후에 하이퍼볼릭탄젠트 함수를 지나도록 하여 출력층 연산을 위한 새로운 벡터인 $\hat{s_t}$를 얻습니다.
어텐션 메커니즘을 사용하지 않는 seq2seq에서는 출력층의 입력이 $t$ 시점의 은닉 상태인 $s_t$였던 반면, 어텐션 메커니즘에서는 출력층의 입력이 **$\hat{s_t}$**가 되는 셈입니다.
식으로 표현하면 다음과 같습니다. $W_c$는 학습 가능한 가중치 행렬, $b_c$는 편향입니다. 그림에서 편향은 생략했습니다.
$\hat{s_t} = tanh(W_c[\alpha_t; s_t] + b_c)$
6) $\hat{s_t}$를 출력층의 입력으로 사용합니다.
$\hat{s_t}$를 출력층의 입력으로 사용하여 예측 벡터를 얻습니다.
앞서 어텐션 메커니즘의 목적과 어텐션 메커니즘의 일종인 닷 프로덕트 어텐션(루옹 어텐션)의 전체적인 개요를 살펴보았고, 바다나우 어텐션 메커니즘과의 차이점은
바다나우 어텐션 메커니즘은 컨텍스트 벡터와 현재 시점의 입력인 단어의 임베딩 벡터를 연결(concatenate)하고, 현재 시점의 새로운 입력으로 사용하는 모습을 보여줍니다. 그리고 이전 시점의 셀로부터 전달받은 은닉 상태 $s_{t−1}$와 현재 시점의 새로운 입력으로부터 $s_t$를 구합니다. 기존의 LSTM이 임베딩된 단어 벡터를 입력으로 하는 것에서 컨텍스트 벡터와 임베딩된 단어 벡터를 연결(concatenate)하여 입력으로 사용하는 것이 달라졌습니다.
이후에는 어텐션 메커니즘을 사용하지 않는 경우와 동일합니다. $s_t$는 출력층으로 전달되어 현재 시점의 예측값을 구하게 됩니다.
여기까지가 해당 논문 내용 리뷰였습니다. 감사합니다. 잘못된 내용 있으면 지적 부탁드립니다.
'Review > Paper' 카테고리의 다른 글
| [논문 리뷰] Prismer: A Vision-Language Model with An Ensemble of Experts (0) | 2023.03.20 |
|---|---|
| [논문 리뷰] Attention Is All You Need (0) | 2023.01.04 |
| [논문 리뷰] Automatic Data Augmentation for Generalization in Reinforcement Learning (0) | 2022.12.16 |
| [논문 리뷰] Batch Normalization: 논문으로 공부하고 이해하기 (0) | 2022.10.17 |
| [논문 리뷰] Deep Networks with Stochastic Depth (0) | 2022.08.21 |
- Total
- Today
- Yesterday
- 도커 컨테이너
- 구글드라이브연동
- few-shot learning
- 서버구글드라이브연동
- docker
- 도커 작업
- 리눅스
- 리눅스 nano
- 리눅스 나노
- 딥러닝
- cs231n
- 파이썬 클래스 다형성
- 파이썬
- 리눅스 나노 사용
- 도커
- stylegan
- python
- style transfer
- Unsupervised learning
- 퓨샷러닝
- support set
- CNN
- 파이썬 클래스 계층 구조
- Prompt
- 프롬프트
- 파이썬 딕셔너리
- prompt learning
- NLP
- linux nano
- clip
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

