티스토리 뷰
이번 포스팅은 standford university의 cs231 lecture 7를 공부하고, 강의와 슬라이드를 바탕으로 정리한 글임을 밝힙니다. 강의 슬라이드는 [Index of slides in 2022] 에서 다운 받을 수 있습니다.
이때까지 배운 것을 살짝 정리해보면, Neural network를 배웠고, Forward/Backword propagation, Update parameters, Convolution layer, CNN architectures 등을 배웠습니다.
이번 강의의 개요는 학습 전 설정, 학습 후 설정, 평가할 때 쓸 수 있는 기법 등이 있습니다.
1. Activation Function

activation function은 활성화함수라고 부릅니다. 이는 neural network에서 데이터의 복잡한 패턴을 학습할 수 있게 도와줍니다. 해당 노드의 출력을 활성화하여 정의하는 함수입니다.

이럴 우리 뇌에 있는 neuron 기반 모델과 비교를 하면 위 그림처럼 나타낼 수 있습니다. 다음 뉴런으로 실행할 학목을 결정하게 됩니다.

조금 더 자세히 살펴보면 이렇습니다. x1,…,xm의 입력값이 있고, 가중치와 곱해지고 bias랑 더해집니다. 그 다음에 해당 값이 activation function에 입력값으로 들어가서 ˆy의 출력값이 나오게 됩니다.
이제 종류를 하나씩 살펴보겠습니다.
Sigmoid Activation Function

시그모이드 함수입니다.
f(z)=11+e−z
시그모이드 함수의 출력 범위는 0과 1 사이입니다. 0과 1사이에 있으므로 각 뉴런의 출력을 정규화합니다. 이는 확률을 출력으로 예측해야하는 모델에서 사용됩니다. 확률은 0과 1 사이의 값만 존재하므로 시그모이드의 선택이 적당했던 것입니다.
그리고 s 곡선 모양의 함수로 gradient가 부드러워지는데, 이는 출력값이 갑자기 확 튀게 하지 않는 걸 의미합니다. 또한, 미분이 가능합니다.
이 함수는 단점이 명확히 있는데, 딥러닝의 가장 큰 문제점인 gradient vanishing 문제가 발생합니다. 이를 미분했을 경우,

이와 같은 그림이 나오는데 만약 입력값이 너무 크거나 작으면 도함수의 값이 현저히 작아집니다. gradient가 이렇게 계속적으로 작아지면, 학습하는데 어려움이 있습니다. 학습을 통해 계속 가중치를 업데이트 시켜야하는데 gradient가 사라지면 학습이 부족하게 됩니다.
함수 출력이 0이 중심이 아닙니다. 이 말은 출력값이 0과 1 사이의 범위이기 때문에 0이 중심이 될 수 없다는 걸 의미합니다. 데이터의 출력값이 0을 중심이 될 경우, 가중치를 업데이트하는데 더 효율적이기 때문에 zero-centered가 중요한 점이 됩니다.
또한, 시그모이드는 지수라서 연산이 느립니다.
Tanh
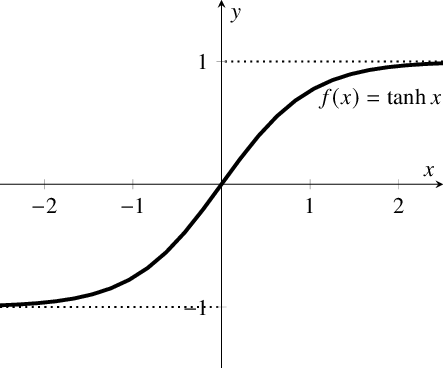
식은 아래와 같습니다.
f(x)=tanh(x)=21−e−2x−1
시그모이드와 유사하게 생겼습니다. 그러나 시그모이드에 비해 몇 가지 이점이 더 존재합니다.
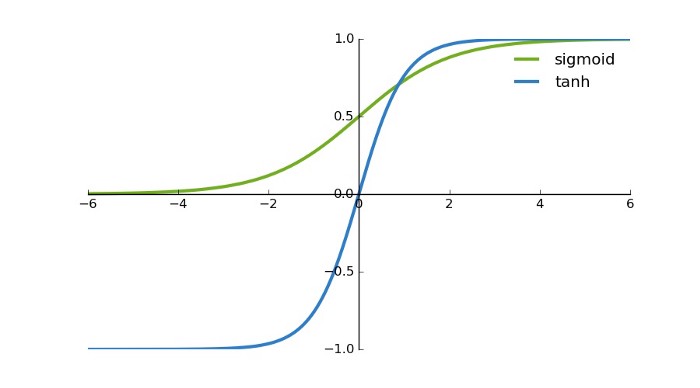
- Sigmoid
- Tanh
Tanh는 출력값이 -1에서 1 사이입니다. 출력 범위가 더 크기 때문에, 가중치를 업데이트 하는 과정에서 더 도움이 됩니다. 음수값도 있기 때문에, gradient가 vanishing되거나 exploding하는 것을 좀 덜하게 잡을 수 있습니다.
또한, 전체 함수가 0 중심으로 시그모이드 보다 좋습니다. 그렇다고 무조건 Tanh를 사용하진 않습니다. 일반적인 분류 문제에서 tanh는 hidden layer에서 사용되며, sigmoid는 output layer에서 사용됩니다. (다중 분류라면 softmax가 사용됩니다.)
ReLU(Rectified Linear Unit)
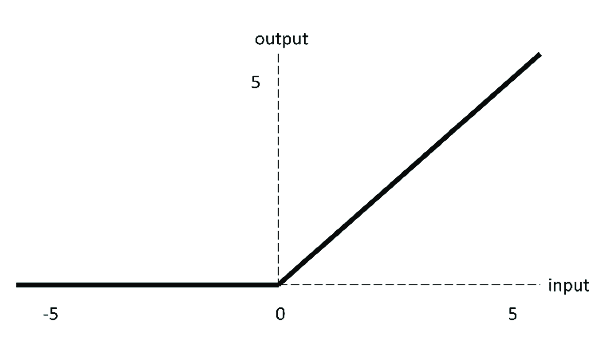
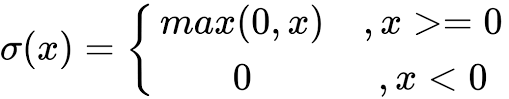
ReLU는 절반이 rectify 되었습니다. f(x)는 x가 0보다 작으면 0, 0보다 크면 같은 값 x가 나옵니다. 따라서 출력 범위는 0에서 무한대입니다.
ReLU는 딥러닝에서 현재 가장 많이 사용되는 활성화 함수입니다.
1. 입력이 양수일 경우, gradient가 saturation 되는 문제가 없습니다.
2. 계산 속도가 훨씬 빠릅니다. ReLU는 선형 관계만 있으므로 forward이든 backward이든 훨씬 빠릅니다.
단점도 존재합니다.
1. Dead ReLU - 입력이 음수이면 ReLU가 완전히 비활성화 됩니다. 그래서 죽는다는 표현을 씁니다. forward pass에서는 문제가 되지 않지만, 역전퐈 과정에서 음수가 입력될 경우, gradient가 0이 되어서 sigmoid나 tanh에서 발생했던 gradient vanishing 문제가 발생합니다.
2. ReLU 함수의 출력은 0 또는 양수입니다. 따라서 ReLU도 zero-centered가 아닙니다.
이런 문제를 개선하기 위해 ReLU를 개선한 많은 활성화 함수가 나왔습니다.
Leaky ReLU
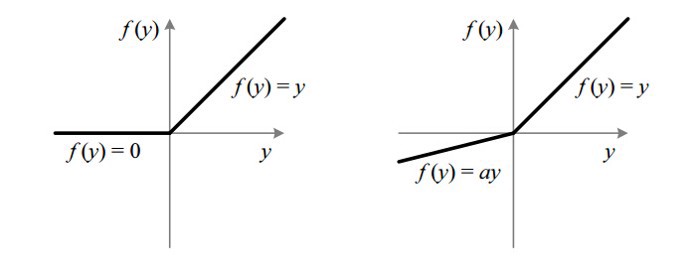
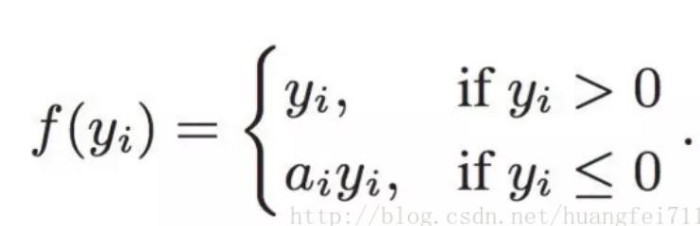
Leaky ReLU의 식입니다.
Leaky ReLU는 x의 매우 작은 값 ai를 통해 음수 입력에 대해 0이 되는 gradient 문제를 조절합니다. 따라서 ReLU의 범위를 늘리는데 도움이 되고, 일반적으로 0.01 정도를 사용합니다. 따라서 Leaky ReLU의 범위는 -무한대에서 무한대가 됩니다.
이론적으로는 Leaky ReLU가 ReLU의 모든 장점을 갖고 있지만, Dead ReLU를 개선하였지만 실제 작동에서는 Leaky ReLU가 항상 ReLU보다 낫진 않습니다.
ELU(Exponential Linear Units)
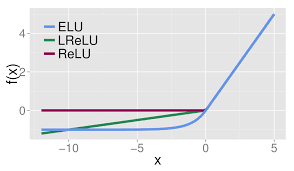
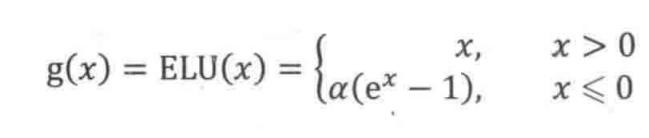
마찬가지로 Dead ReLU의 문제를 해결하기 위해 제안되었습니다.
활성화 평균이 0에 가깝게 만드는 음수값을 갖습니다. 0에 가까운 평균 활성화는 기울기를 더 가깝게 가져와서 더 빠른 학습을 가능하게 합니다.
Leaky ReLU와 비교했을 때, 음수값에서 saturation 되는 걸 노이즈에 약간의 robustness를 추가해줍니다. 하지만 지수 함수를 계산해야 합니다.
SELU(Scaled Exponential Linear Units)
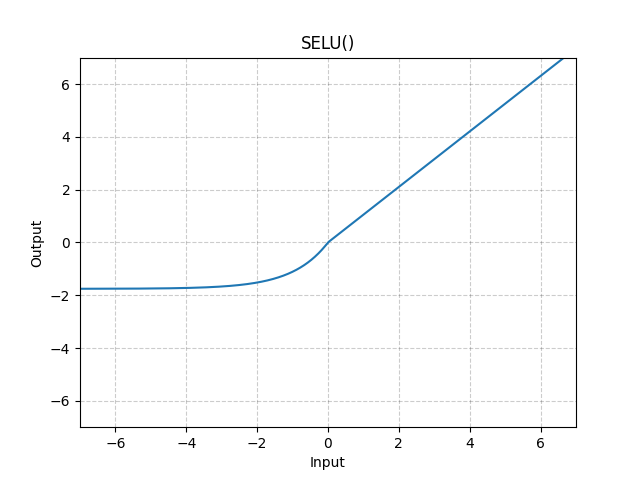
조금 신기하게 생겼습니다. 식은 아래와 같습니다.
SELU(x)=scale∗(max(0,x)+min(0,α∗(exp(x)−1)))
ELU와 다른 점은 여기서 scale을 조정하는 λ가 추가되며, α 또한 이전과 동일하게 존재합니다. 얘는 self-normalizing하는 특성이 있으며, BatchNorm 없이 SELU network를 학습할 수 있습니다.
파이토치 사이트의 설명을 참고하면, 가중치 초기화를 위해 kaiming_normal을 사용할 때, Self-Normalizing Neural Networks을 얻기 위해 대신 사용한다고 합니다.
Self-Normaliziong의 개념은 처음 들어보는데 2017년에 나온 Self-Normalizing Neural Networks이란 관련 논문이 있습니다. 배치 정규화에서 정규화가 이뤄지지만, SNN의 뉴런 활성화는 자동으로 평균 0, 분산 1로 수렴된다고 합니다. 따라서 자체 정규화 속성을 유도한다 하여 scaled exponential linear units(SELU)이라 부릅니다.
결국 ReLU 친구들을 모두 정리해주면
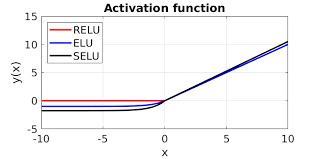
이렇습니다.
활성화 함수는 여기까지 살펴보겠습니다.
2. Data Preprocessing
데이터를 전처리하는 기본적인 내용입니다. 전처리는 raw data에 대한 모든 변환을 의미합니다. 예를 들어, raw data 그대로 cnn을 훈련하면 분류 성능이 떨어질 수 있는데, 전처리는 성능을 높이는데 중요성을 차지하고 있습니다.
크게 분산과 공분산에 대한 개념 이해와 평균 정규화(mean normalization), standardization에 대해 살펴볼 것입니다.
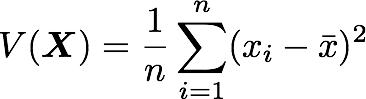
분산의 공식은 위와 같습니다. 벡터의 길이가 n, 평균은 ˉx입니다.
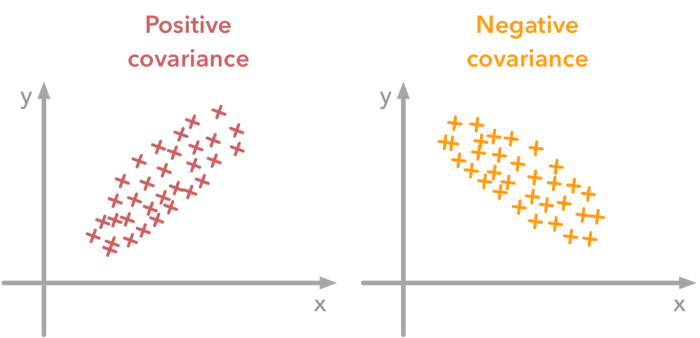
분산은 값이 분산된 정도를 나타내며, 공분산은 두 변수 간의 종속성을 나타내는 척도입니다. 양의 공분산은 두 번째 변수의 값이 클 때 첫 번째 변수 값이 크다는 것을 의미하며, 양의 공분산은 반대입니다.
공분산의 값은 변수의 척도에 따라 달라지므로 분석하기 어렵고, 상관 계수를 통해 해석할 수 있습닏나.

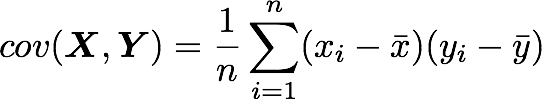
공분산 식은 위와 같습니다.
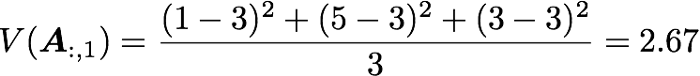
A 행렬의 첫 번째 열 벡터의 분산을 구했습니다.
평균으로 정규화하는 방법은 각 sample에서 평균을 제거하는 방법입니다.
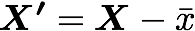
X′가 정규화 된 dataset이며, X가 데이터 세트, ˉx는 평균입니다.
standardization은 위의 값에서 표준편차로 나눈 경우를 의미합니다.
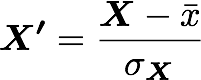
X′가 정규화 된 dataset, X가 데이터 세트, ˉx는 평균, σx가 x의 표준편차입니다.
3. Weight Initialization
가중치를 초기화하는 이유는 무엇일까요? Deep neural network를 통한 forward pass 과정에서 layer마다 활성화 된 출력값이 exploding/vanishing 되는 것을 방지하기 위함입니다. gradient가 너무 크거나 작으면 backward pass시에 수렴하는데도 오래 걸립니다.
- Small random numbers
먼저 작은 값으로 업데이트 하는 경우를 살펴보겠습니다. 가중치의 표준편차를 0.01로 바꿔 실험을 진행합니다. 학습은 수행되지만 문제는 레이어가 깊어질 때입니다.

깊어질수록 모든 활성화 값이 0으로 수렴하게 됩니다.
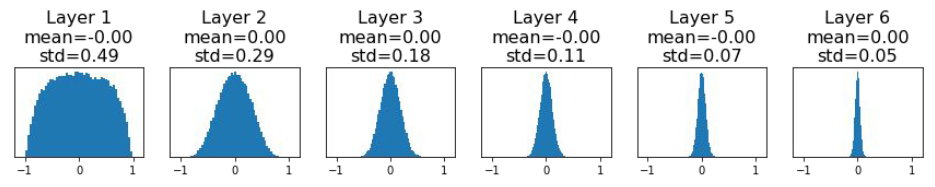
0이 된다는 것은 더 학습할 수 없다는 것을 의미합니다.
이렇게 활성화 값이 치우치게 되면 다수의 뉴런이 거의 같은 값을 출력하고 있다는 것을 의미하고, 많은 뉴런을 가진 이점이 사라진다는 뜻입니다. 따라서 이렇게 작은 값으로 초기화하여 활성화 값이 치우치게 되면 표현력를 제한한다는 관점에서도 문제가 발생됩니다.
각 층의 활성화 값은 적당하게 고루 분포되는 것이 좋습니다. 레이어 사이에 적당하게 다양한 데이터가 흘러야 신경망 학습이 효율적으로 이뤄집니다. 반대로 치우친 데이터가 흐르면 기울기 소실, 표현력 제한 문제에 빠져 학습이 잘 이뤄지지 않습니다.
- Large random numbers
반대로 큰 값의 경우를 살펴보겠습니다. 0.01에서 0.05로 올렸습니다.

그랬더니 활성화 분포가 완전 퍼져버리는 saturation 현상이 발생합니다. activation 값이 굉장히 크거나 작아지게 된 것입니다. 이 경우도 마찬가지로 학습이 어렵습니다.
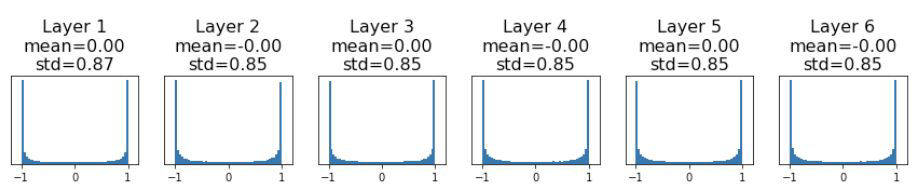
그래서 그 다음으로 제안된 초깃값 방법은 활성화 값들을 더 넓게 분포시킬 목적으로 적절한 분포를 찾고자 했습니다.
- Xavier
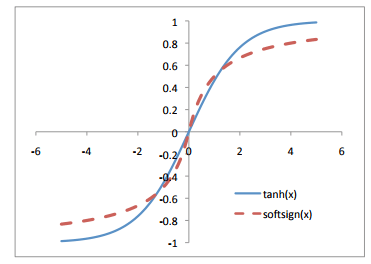
이전에 가장 일반적으로 사용되는 활성화 함수는 주어진 값에 대한 대칭을 이뤘습니다. tanh나 softsign function이 해당됩니다.
가중치가 1/√n으로 조정되는 방법이 Xavier 초기화 방법입니다. 이건 2010년쯤에 weight layer를 초기화하는 방법이었다고 합니다.
layer가 가진 노드의 개수 n개에 맞게 나눠주어 노드가 많을수록 초깃값으로 설정하는 가중치가 좁게 퍼집니다.


Xavier 초기화 방법을 사용한 결과는 위 그림과 같습니다. 층이 깊어지면서 형태가 바뀌고 있는데, 앞에서 본 것과 비교했을 땐 확실히 더 넓게 분포됩니다. 각 층에 흐르는 데이터가 적당히 퍼져 있으므로 시그모이드 함수의 표현력도 제한 받지 않고 학습이 더 효율적으로 이뤄지게 됩니다.
- ReLU
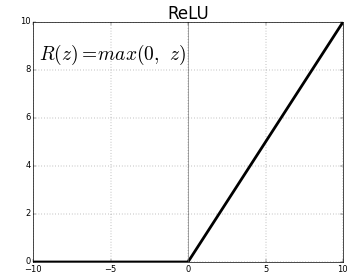
ReLU로 초기화를 하면 어떨까요? Xavier 초깃값은 활성화 함수가 선형인 것을 전제로 이끈 결과였습니다. 시그모이드와 하이퍼볼릭탄젠트 함수도 좌우 대충이라 중앙 부근이 선형인 함수입니다. 따라서 Xavier 초깃값이 적절합니다.
반면 ReLU를 활성화 함수로 이용할 때는 다른 초기화 방법이 더 적절할 수 있습니다. ReLU를 활성화 함수로 사용했을 경우의 Xavier 초깃값 시켰을 때를 살펴보겠습니다.

가중치가 Xavier로 초기화되고 ReLU 함수를 적용한 x의 output이 나옵니다. 이 x를 히스토그램으로 표현해보면 아래와 같습니다.

ReLU의 경우,actiations이 0으로 collapse하며 local gradient가 0이 되어 학습이 진행되지 않습니다. x가 zero-centered되지 않은 상태이기 때문입니다.
- Kaiming
따라서 Kaiming He가 ReLU를 사용할 때의 가중치 초기화 방법을 제안합니다. 이 방법은 이름을 따서 He 초깃값이라고 주로 부릅니다.
앞 계층의 노드가 n개일 때, 표준편차가 √ 2/ n 인 정규분포를 사용합니다. ReLU는 음의 영역이 0이라서 더 넓게 분포시키기 위해 Xavier에서 사용한 1/√n 의 제곱 안에 2를 더 곱했습니다.

코드와 아래의 히스토그램을 통해 변화를 살펴볼 수 있습니다. 활성화의 출력이 사라지거나 폭발해버리는 것을 방지할 수 있게 되었습니다.

ReLU와 같은 활성화를 사용하여 네트워크에서 가중치를 가장 잘 초기화하는 방법에 대한 이러한 탐색은 Kaiming He가 제안하였고, 이러한 종류의 비대칭, 비선형 활성화를 사용하는 Deep neural network에 맞게 조정된 자체 초기화 방법입니다.
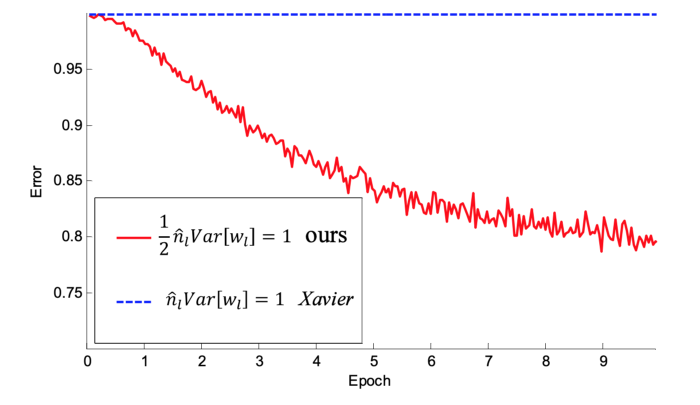
2015년에 나온 논문에서 해당 방법을 통해 22 layers를 가진 CNN이 훨씬 더 일찍 수렴됨을 보여주기도 합니다. 이는 Xavier와 He 초깃값 방법을 사용했을 때의 비교 그래프입니다. Xavier의 경우, 학습이 아예 중단되었습니다.
4. Training vs. Testing Error
- Training error
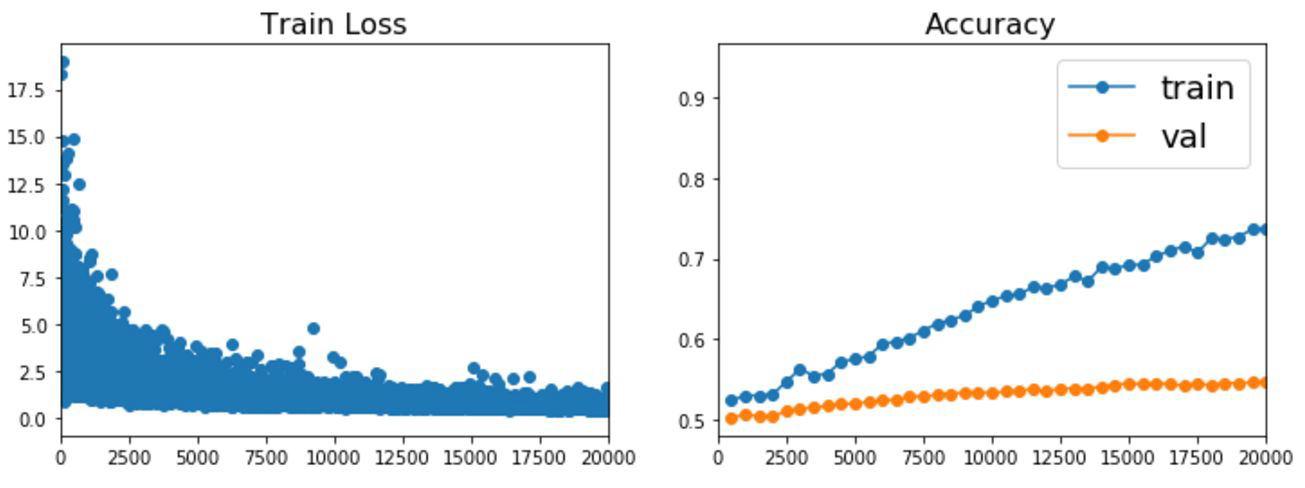
- training loss가 줄여주는 가장 좋은 최적화 알고리즘을 찾아야 함
- training accuracy와 validation accuracy를 지켜보며 차이가 커지지 않게, overfitting 되는지를 확인해야 함
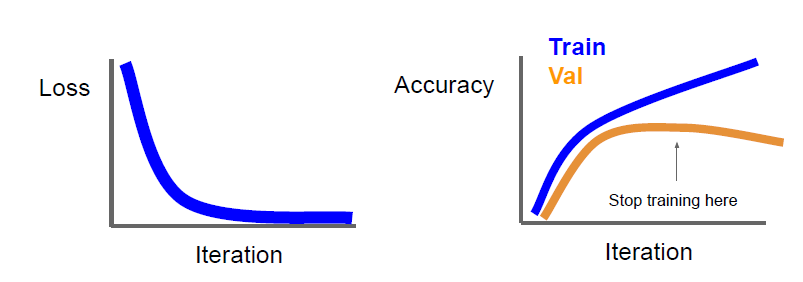
학습이 제대로 되고 있지 않다고 판단될 때 멈출 수 있습니다. 이를 Early stopping 또는 조기 종료라 그럽니다.
train dataset의 정확도는 계속 올라가는데, validation 정확도가 떨어지기 시작했다면 학습을 종류 시킬 수 있습니다.
각각의 모델을 여러 개 Ensemble 할 수도 있습니다. 그리고 test time에서 이 결과를 평균냅니다.
이렇게 learing process를 지켜보고 parameter update를 돕는 기법을 통해 더 나은 학습의 결과로 이끌 수 있습니다. 뒤에서 이어집니다.
5. Improve model performance

위에서도 learning process를 보는 가장 중요한 이유는 overfitting을 피하는 것이었습니다. 그 방법으로 Regularization(정규화)가 있습니다. 여기엔 다양한 기법이 존재합니다.
과적합은 신경망이 훈련 중에 데이터의 기본 개념으로 학습하는 훈련 데이터의 노이즈로 인해 발생합니다. 이 노이즈의 편차를 줄이기 위해 위의 방법을 통해 어느 정도 해결할 수는 있었습니다.
그러나 이 학습된 노이즈들은 각 훈련 세트마다 고유합니다. 배치마다 고유할 수도 있습니다. 모델이 동일한 문제 영역의 새 데이터를 보았지만 여기에 이 노이즈가 포함되어 있지 않으면 신경망의 성능이 훨씬 나빠집니다.
신경망이 노이즈를 학습하는 이유로는 네트워크의 복잡성이 너무 크기 때문입니다.
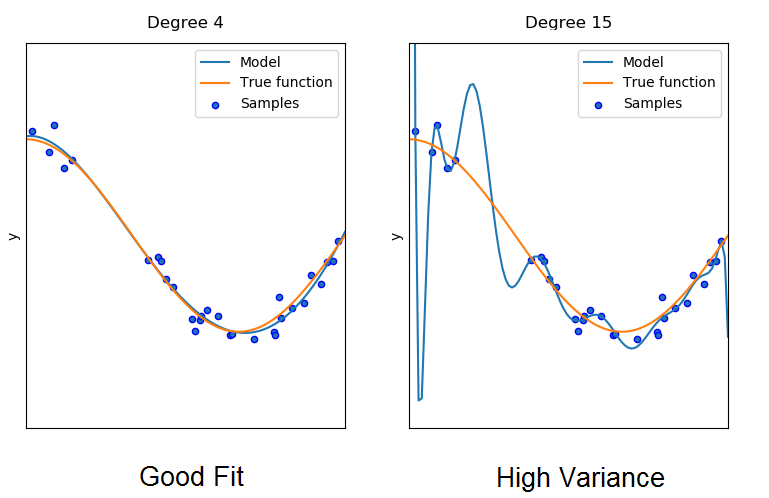
복잡성이 더 높은 모델은 임의의 변동 또는 오류로 인해 발생하는 데이터의 패턴(노이즈)을 선택하고 학습할 수 있습니다. 네트워크는 분포를 설명하는 실제 함수를 인식하지 못한 채 분포의 각 데이터 샘플을 하나씩 모델링합니다.
True function으로 생성된 새로운 임의 샘플은 모델의 적합도와 거리가 멀어집니다. 이때를 모델의 분산이 높다고도 말합니다.
반면에 왼쪽의 복잡성이 낮은 네트워크는 각 데이터 패턴을 개별적으로 모델링하는 데 너무 많은 노력을 기울이지 않음으로써 분포를 훨씬 더 잘 모델링합니다. 실제로 과적합은 신경망 모델이 훈련 중에 매우 잘 수행되도록 하지만 새로운 데이터에 직면할 때 추론 시간 동안 성능이 훨씬 더 나빠집니다.
간단히 말해서 정규화는 과적합이나 높은 분산을 방지하기 위해 필요하며, 신경망 모델의 복잡성을 낮추고 과적합을 방지하는 다양한 technique라 볼 수 있습니다.
- Add term to loss
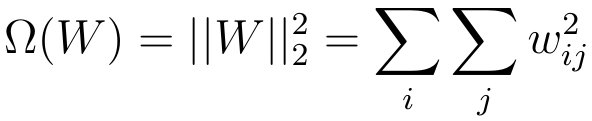
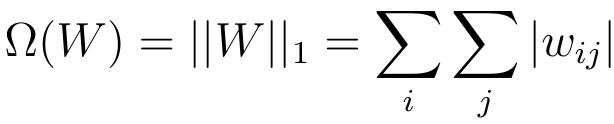
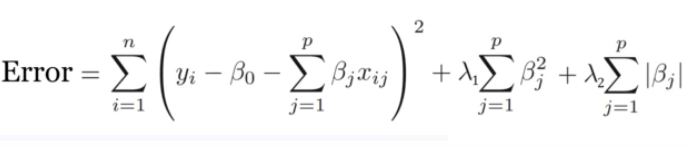
- Dropout
dropout은 훈련 중에 어느 정도 확률 p로 신경망의 뉴런이 훈련 중에 꺼지는 것을 의미합니다. 아래 그림을 통해 이해할 수 있습니다.
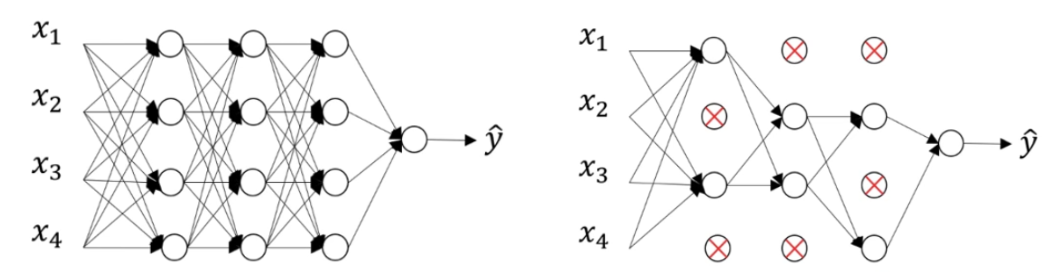
왼쪽에 드롭아웃이 없는 피드포워드 신경망이 있다고 가정합니다. 학습 중에 임의의 뉴런이 꺼지는 P=0.5의 확률로 드롭아웃을 사용 하면 오른쪽에 신경망이 생성됩니다.
이 경우 뉴런의 약 절반이 활성화되지 않고 신경망의 일부로 간주되지 않는 것을 관찰할 수 있습니다. 그리고 관찰할 수 있듯이 신경망은 더 간단해집니다.
신경망의 단순한 버전은 과적합을 줄일 수 있는 복잡성을 줄입니다. 특정 확률 P를 가진 뉴런의 비활성화는 각 순방향 전파 및 가중치 업데이트 단계에서 적용됩니다.
이는 Training과 Testing 때 어떻게 이용하는지 이해하면 더 좋습니다.
- training 때는 각 hidden layer, 각 training sample에 대해 각 반복마다 노드의 임의 부분을 p로 zero out 시킵니다.
- test 때는 모든 활성화를 사용하지만 p만큼 줄입니다. 훈련 중에 누락된 활성화를 설명하기 위해 이렇게 조절합니다.
- Dropout은 신경망이 다른 뉴런의 여러 무작위 하위 집합과 함께 유용한 더 강력한 기능을 학습하도록 합니다.
- Dropout은 수렴에 필요한 반복 횟수를 대략 두 배로 늘립니다. 그러나 각 Epoch에 대한 training time은 더 적습니다.
- H개의 은닉 유닛을 사용하여 각각 드롭할 수 있으므로 2H개의 가능한 모델이 있습니다. 테스트 단계에서 전체 네트워크가 고려되고 각 활성화는 p 만큼 감소합니다 .
정리
- overfitting은 더 복잡한 신경망 모델(많은 레이어, 많은 뉴런)에서 발생합니다.
- L1 및 L2 정규화와 드롭아웃을 사용하여 신경망의 복잡성을 줄일 수 있습니다.
- L1 정규화는 가중치 매개변수를 0으로 만듭니다.
- L2 정규화는 가중치 매개변수를 0으로 강제합니다(그러나 정확히 0은 아님).
- 가중치 매개변수가 작을수록 일부 뉴런을 무시할 수 있음 → 신경망이 덜 복잡해짐 → 덜 overfitting 됨
- 드롭아웃 동안 일부 뉴런은 무작위 확률 P 로 비활성화 됨 → 신경망이 덜 복잡해짐 → 덜 overfitting 됨
- Data Augmentation
이 기법은 기존 데이터에서 추가 데이터를 생성할 수 있습니다. 더 많은 실제 데이터를 수집하기 어려울 때 모델 정확도를 개선하고 시간과 비용을 절감합니다.
따라서 기존 데이터에서 새로운 훈련 데이터를 생성하여 원래 데이터 세트를 확장하는 기술입니다.
- Horizontal Flips: 좌우 대칭
- Random Crops and Scales
- Training: sample random crops / scale
- Testing:average a fixed set of crops
- Color jitter: Lightness(밝기), Hue(색상), saturation(채도) 등을 임의로 변경 / 이는 RGB 색 모델의 다른 표현 방법입니다.
- Rotation
- Cropping
- Zooming
- Scaling
- Translation
- Adding noise
- Fractional Pooling: pooling region인 receptive filed 크기를 랜덤하게 설정하는 방법
- Stochastic Depth: residual block을 랜덤하게 drop하는 방법
- cutout: 랜덤하게 이미지를 0으로 만듦
- mixup:이미지를 blend weight에 따라 blend하는 방법입니다.
- Drop Connect
해당 방법도 dropout과 마찬가지로 특정한 뉴런에 의존하지 않도록 독립적인 특징을 추출하기 위해 사용합니다. 같은 방식이지만 Dropconnect는 weights를 비활성화 시키고 node는 그대로 활성화 시키는 방법입니다.
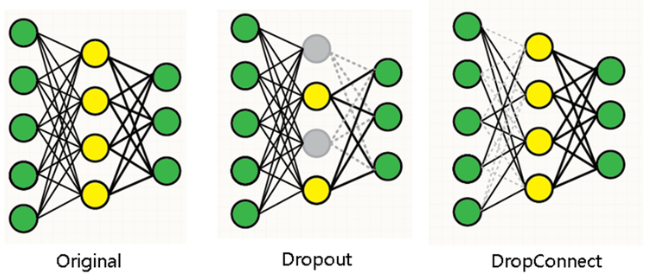
- Original: 모든 노드와 가중치 사용
- Dropout: 일부 뉴런 비활성화
- Dropconnect: connection을 생략하여 노드는 남아 있고, weight를 생략
성능으로는 파라미터가 일종의 동조(co-adaptation)하는 것을 막는다는 관점에서 dropout과 dropconnect는 비슷합니다. 하지만 dropconnect가 dropout을 더 일반화 시킨 버전으로 이해를 할 수 있으며, connection만 생략해서 훨씬 가능한 모델이 더 많이 나온다는 차이점이 있습니다.
이론적으로는 DropConnect가 자유도(표현력)이 높아서 Dropout보다 더 좋아야 할 것 같지만, 약간 좋은 수준이고 데이터마다 차이가 존재해서(해당 논문을 바탕으로) 이 방법이 보편적으로 사용되는 것 같지는 않습니다.
이 방법보다 신경망에서는 overfitting이 가장 큰 문제이며, 이 문제를 해결하기 위한 regularization 방법이 중요함에 따라 다양한 기법이 나왔다고 흐름을 이해하였습니다.
데이터 증강의 이점을 정리해보면
- 데이터 수집 및 데이터 라벨링 비용 절감
- 모델에 더 많은 다양성과 유연성을 부여하여 모델 일반화 개선
- 모델 학습에 더 많은 데이터가 사용됨에 따라 예측에서 모델 정확도 향상
- 데이터의 과적합 감소
- 소수 클래스의 샘플을 보강하여 데이터 세트의 불균형 처리
입니다.
6. Choosing Hyperparameters
이제 진짜 마지막입니다.
Step 1: Check initial loss
Step 2: Overfit a small sample
Step 3: Find LR that makes loss go down
Step 4: Coarse grid, train for ~1-5 epochs
Step 5: Refine grid, train longer
Step 6: Look at loss and accuracy curves
해당의 스텝으로 하이퍼 파라미터를 튜닝합니다.
Summary
- Improve your training error:
- Optimizers
- Learning rate schedules
- Improve your test error:
- Regularization
- Choosing Hyperparameters
Reference
[1] https://medium.com/analytics-vidhya/activation-functions-all-you-need-to-know-355a850d025e
[3] https://towardsdatascience.com/regularization-in-deep-learning-l1-l2-and-dropout-377e75acc036
[6] 밑바닥부터 시작하는 딥러닝 1
'AI > CS231n' 카테고리의 다른 글
| cs231n 9강 정리 - Object Detection and Image Segmentation (4) | 2023.01.17 |
|---|---|
| cs231n 8강 정리 - Visualizing and Understanding (0) | 2022.12.05 |
| cs231n 5강 정리 - Convolutional Neural Networks (0) | 2022.08.15 |
| cs231n 4강 정리 - Introduction to Neural Networks (0) | 2022.08.15 |
| CS231n 3강 정리 - Loss Functions and Optimization (0) | 2022.08.14 |
- Total
- Today
- Yesterday
- 파이썬 딕셔너리
- 퓨샷러닝
- 구글드라이브연동
- NLP
- 프롬프트
- 도커 작업
- clip
- 리눅스 나노
- docker
- stylegan
- 서버구글드라이브연동
- support set
- 파이썬 클래스 다형성
- style transfer
- 도커 컨테이너
- 도커
- 딥러닝
- 리눅스 나노 사용
- python
- 리눅스
- linux nano
- 리눅스 nano
- prompt learning
- cs231n
- Prompt
- Unsupervised learning
- CNN
- 파이썬
- few-shot learning
- 파이썬 클래스 계층 구조
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

