티스토리 뷰
이번 포스팅은 standford university의 cs231 lecture 4를 공부하고, 강의와 슬라이드를 바탕으로 정리한 글임을 밝힙니다.
제가 직접 필기한 이미지 자료는 별도의 허락 없이 복사해서 다른 곳에 게시하는 행위를 금지합니다. 필요하신 경우 댓글로 알려주세요!
Reference
💻 유튜브 강의: Introduction to Neural Networks
💻 한글 강의: cs231n 4강 Backpropagation and NN part 1
📑 slide: PDF
Contents
- Reference
- Contents
- Review
- Backpropagation: a simple example
- Another example
- Patterns in backward flow
- Gradients add at branches
- Vectorized operations
- A vectorized example
- Neural Networks
- Artificial Neural Network
- Activation Function
- Neural networks: Architectures
- Example feed-forward computation of a neural network
- Summary
Review
저번 시간 강의를 간단히 review 하겠습니다. 지난 시간 classifier을 정의하는 함수 $f$에 대해 공부했습니다.
함수 $f$는 데이터 $x$가 입력 $input$이며, weight $W$를 parameter로 갖고 출력 $output$은 분류하고자 하는 class들의 $score$ $vector$로 표현되었습니다.
또한, loss function을 정의내리며 SVM loss function을 예로 들었는데요. 여기선 $data$ $term$과 $regularization$ $term$을 합쳐 $total$ $Loss$를 구할 수 있었습니다.

여기서 이제 최적의 loss를 갖는 parameter $W$를 찾기 위해 loss function의 $W$에 대한 gradient를 통해 $optimization$의 과정까지 살펴보았습니다.
gradient를 구하는 finite difference approximation을 통한 계산 방법도 보았는데요. 속도가 느리고 근사치를 찾는 방법이 Numerical Gradient였습니다.
대신 빠르고 정확한 analytic gradient 방법이 있지만 실수하기 쉽다는 단점도 있었습니다. 이 둘 중 더 많이 사용하는 것은 analytic gradient의 방법입니다.
이번 lecture 4에서는 analytic gradient 계산 방법에 대해 다룰 예정입니다. 그때 computational graph라고 부르는 framework를 사용할 예정이며, 그래프의 각 노드는 연산 단계를 보여줍니다.

computational graph을 사용하게 되면서 함수는 $backpropagation$이라는 기술을 사용할 수 있게 되는데요. backpropagation은 gradient를 얻기 위해 computational graph 내부의 모든 변수에 의해 chain rule을 재귀적으로 사용하게 됩니다.

Backpropagation: a simple example
💻 오차역전파 (Backprogation)의 개념을 쉽게 이해해 봅시다
강의에서는 Backpropagation을 아주 간단한 함수를 통해 계산하는 예를 보여줍니다.
위 영상은 강의에서 다룬 똑같은 simple example을 풀이해주는 한국어 강의입니다. cs231n 강의가 어렵게 느껴지신 분들은 위 영상을 참고하시길 바랍니다.
chain rule이 무엇인가?
chain rule은 합성함수의 미분할 때 사용하는 공식을 의미합니다. 이를 잘 모르겠는 분은 연쇄 법칙 - 위키백과을 참고해주세요.


Backpropagation을 알기 전에 알아야하는 것은 Forward Pass라고 생각하는데요. Forward Pass는 순방향으로의 계산 방식을 의미합니다. 그럼 반대는 무엇일까요?
당연히 Backward Pass가 되겠죠. 이는 Backpropagation이라고도 불립니다. 우리가 오늘 공부할 오차 역전파인거죠.
위에서는 아주 간단한 함수를 제공합니다.
$f(x,y,z) = (x+y)z$
$q=x+y$
$f=qz$
$x=-2, y=5, z=-4$
입니다.

빨간색 네모 박스를 봐주세요. $q$ 식에 대한 $x$의 미분, $q$ 식에 대한 $y$의 미분을 계산합니다.
$q=x+y$ 식이기 때문에 미분을 계산하면
$\frac{∂q}{∂x}=1$ , $\frac{∂q}{∂y}=1$
이 됩니다.
$f$ 식에 대한 $q$의 미분, $f$ 식에 대한 $z$의 미분의 미분도 어렵지 않습니다. 함수 f는 $f=qz$ 이기 때문에 미분하면
$\frac{∂f}{∂q}=z$ , $\frac{∂f}{∂z}=q$
입니다.
재밌는 건 $q$에 대해 미분하니 $z$가 나오고, $z$에 대해 미분하니 $q$가 나옵니다. 서로 switch하고 있습니다.
어쨌든 우리는 $q$와 $z$ 값을 알고 있습니다. 그래서
$\frac{∂f}{∂q}=z=-4$ , $\frac{∂f}{∂z}=q=3$
의 값을 갖게 되는 것입니다.
그러면 이제 $f$에 대한 $x$로의 미분을 궁금해 할 차례입니다. 근데 $f=qz$이기 때문에 $x$로의 미분이 불가능한데요.
여기서 사용하는 것이 chain rule입니다.

$\frac{∂f}{∂x}=\frac{∂f}{∂q}* \frac{∂q}{∂x}=(-4)*1=-4$
가 됩니다.
이 의미는 x가 1만큼 증가할 때, f가 -4만큼 증가했다. 즉, 4만큼 감소했다는 의미가 됩니다. 이렇게 계산한 이유는 우리는 이미
$\frac{∂f}{∂q}=-4$, $\frac{∂q}{∂x}=1$
임을 알고 있기 때문입니다. 똑같이 $f$에 대한 $y$로의 미분을 살펴보겠습니다.

$\frac{∂f}{∂y}=\frac{∂f}{∂q}* \frac{∂q}{∂y}=(-4)*1=-4$
입니다.
이것도 앞에 계산한 식을 알고 있었기 때문에 쉽게 구할 수 있습니다. 여기서 이제 중요한 개념이 나옵니다.
바로 local gradient랑 global gradient인데요.

이렇게 forward pass 시에 gradient를 구할 수 있습니다. 이를 local gradient라고 합니다. 반대로 backward pass시에 구하는 gradient를 global gradient라고 합니다.
보라색 형광펜으로 박스가 된 부분을 확대해서 살펴보면 우리가 가장 먼저 구했던
$\frac{∂q}{∂x}=1$ , $\frac{∂q}{∂y}=1$
가 local gradient입니다!

forward pass시 우리는 local gradient를 계산할 수 있다.
local gradient를 계산해두면, 아까 chain rule을 이용해서 계산할 때 local gradient를 사용헀던 것이 기억나시나요? backward pass하며 구한 upstream gradient와 곱해서 최종적 gradient 계산시 편리하기 때문입니다.

우리는 굉장히 간단한 graph로만 살펴보았기 때문에 total loss로부터 이미 수많은 계산이 있었다고 가정합니다. 수많은 계산을 거쳐 loss의 q에 대한 미분까지 올 수 있었습니다.
저 식이 global gradient가 되는 것입니다. 그렇다면 이제 다시 정리해보겠습니다.

chain rule*을 활용해 local gradient global gradient를 곱하여 gradient를 계산하게 되는 것입니다.
$\frac{∂Loss}{∂x}=\frac{∂Loss}{∂q}* \frac{∂q}{∂x}=(-4)*1=-4$
$\frac{∂Loss}{∂y}=\frac{∂Loss}{∂q}* \frac{∂q}{∂y}=(-4)*1=-4$
처럼 말이죠.
이 simple example을 통해 알게 된 새로운 개념은
local gradientglobal gradientchain rulegradient=local gradient*global gradient
입니다.
- 아무리 깊고 복잡한 층으로 구성되어 있다고 하더라도 chain rule을 활용해 미분 값을 얻어낼 수 있다.
- Forward Pass시 Local Gradient를 미리 계산한다.
- 저장해둔 Local Gradient와 Global Gradient를 Backward Pass시 곱하여 최종 미분 값을 얻는다.
Another example
강의에서 제시한 another example은

해당 식입니다.
$f(w,x)$ 식은 이미지 왼쪽 상단 부분을 참고 부탁드립니다.

아까 gradient를 구하기 위해 어떻게 했었나요? 바로 local gradient* global gradient 이 공식이었습니다.
우리는 global gradient를 무조건 1로 시작합니다.
$\frac{∂f}{∂f}=1$
이유는 $f$에 대한 $f$의 미분값을 이용하기 때문입니다. 식은 $\frac{1}{x}$입니다. 해당 식을 미분하면 $-\frac{1}{x^2}$가 됩니다.
그래서 해당 $x$ 자리에 local gradient 값인 1.37을 대입하고 global gradient인 1과 곱해줍니다.
$-\frac{1}{1.37^2}* (1.00)=-0.53$
입니다.
위 과정을 반복합니다. 여기서의 계산은 잘 모르겠다 싶으면 skip하거나 정말 이해하고 싶다면 한국어 강의 cs231n 4강 Backpropagation and NN part 1를 추천합니다.

초록색 글씨가 local gradient를 의미하고, 빨간색 글씨가 upstream gradient를 의미합니다.
위에서부터 각 노드를 타고 하나씩 내려오기 때문에 위에서 계산된 gradient를 upstream gradient라고 하나봅니다.
그럼 아까 정리한 걸 더 정확히 다시 표현한다면,
gradient=local gradient*upstream gradient
가 되겠군요.
sigmoid gate
$f(w,x)$ 식이 어떻게 생겼나요?

$\sigma(x)=\frac{1}{1+e^{-x}}$ 와 흡사합니다. $x$ 자리에 $-(w_0x_0+w_1x_1+w_2)$만 대입하면 똑같은 함수입니다. sigmoid function을 미분하면

입니다.
미분 과정은 사실 더 자세히 안 적고 강의 노트 바탕으로만 정리했습니다. 간단하게는 $({1+e^{-x}})^{-1}$ 해당 식의 미분을 정리해보면 나옵니다.
아무튼 여기서 중요한 건 저 노랑색 형광펜 쳐진 부분입니다. sigmoid function이 미분했더니 $(1-\sigma(x)) \sigma(x)$로 유도되었단 사실이죠.

그래서 파란색 네모 박스 부분의 계산은 $(1-\sigma(x)) \sigma(x)$를 이용해서 계산했더니 값이 똑같이 나왔다는 사실입니다.
$(0.73)(1-0.73)=0.2$가 됩니다.
복잡한 계산 과정이 필요없고 이렇게 간단히 나온다는 사실을 알려주고 있습니다.
Patterns in backward flow
gradient를 계산하는 backward 과정에 패턴이 있습니다.
add, max, mul gate
add gate: gradient distributor- 전의 gradient를 그대로 전파. local gradient의 값이 1이라서
- 두 개의 브랜치와 연결되는 덧셈 게이트는 upstream gradient를 연결된 브랜치에 같은 값으로 나눠줌
- 1로 나누면 그대로의 값이 나옴
max gate: gradient router- 여러 개 중에 하나만 취해주기 때문에
mul gate: gradient... ‘switcher?’- local gradient가 바뀌기 때문에
local gradient
local gradient는 forward pass 때 구할 수 있다.
global gradient
- backward pass 동안에만 구할 수 있다.
- 즉, local gradient랑 global gradient를 곱해서 gradient를 구할 수 있다.
- backward pass 때 chain rule이 일어난다.
Gradients add at branches

위 이미지처럼 여러 노드와 연결되어 있는 하나의 노드가 있을 때, gradient는 노드를 합산됩니다. upstream gradient 값을 취하고, 그 값을 합칩니다. 그러면 이 과정이 다변수 chain rule로 바라볼 수 있습니다.
$\frac{∂f}{∂x}=Σ\frac{∂f}{∂q_i}* \frac{∂q_i}{∂x}$
Vectorized operations
이제 벡터라면 어떻게 될지 생각해봅시다. 변수 $x,y,z$에 대해 숫자 대신 vector를 가지고 있다고 가정합니다.
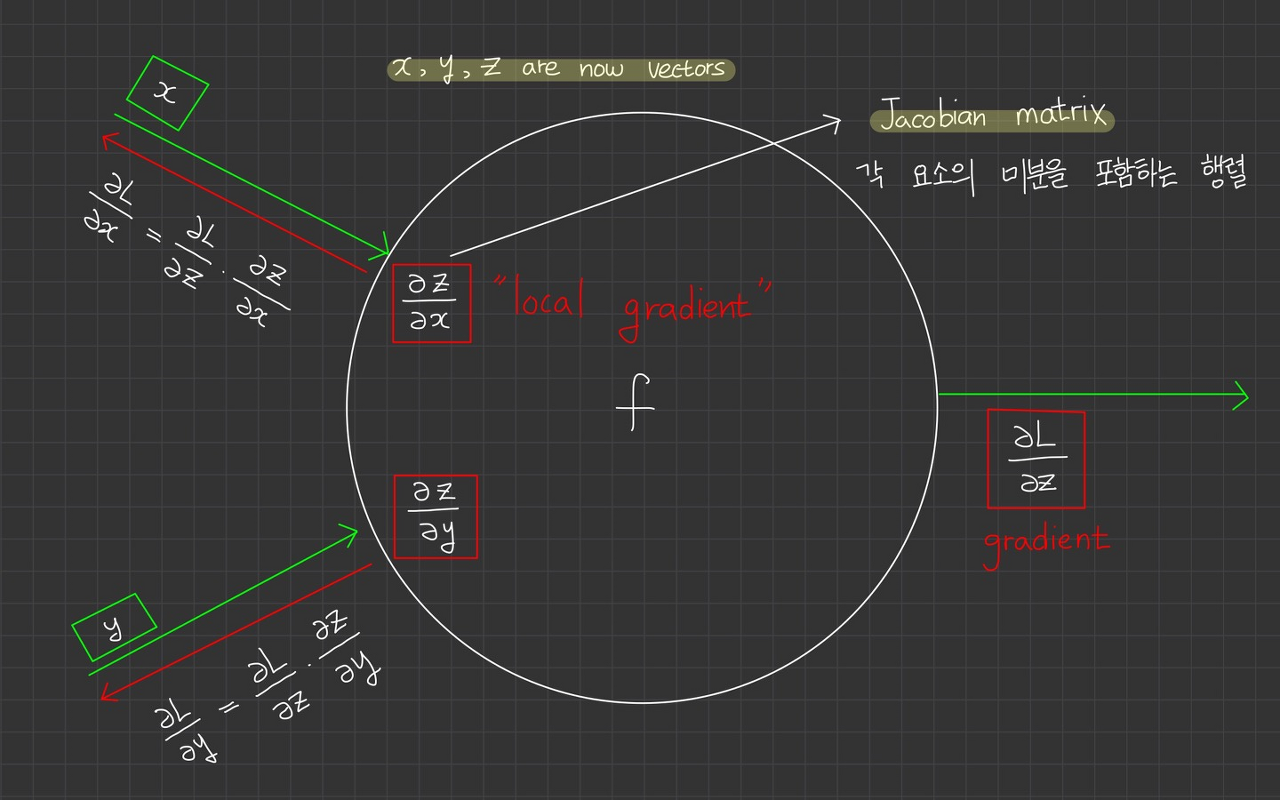
gradient는 Jacobian 행렬이 됩니다. 예를들어, $x$의 각 원소에 대해 $z$에 대한 미분을 포함하는 행렬이 됩니다.
*Jacobian 행렬은 야코비 행렬이라고 합니다. 한국에서 번역 과정에서 자코비안이나 야고비나 다양하게 불리는 것 같습니다.
예시를 하나 또 들어줍니다.

4096 차원의 input vector가 있습니다. 이 노드는 요소별로 최대값을 취해줍니다.
output 또한 4096 차원의 vectore입니다. 이 경우의 Jacobian 행렬 사이즈는 어떻게 될까요?
Jacobian 행렬의 각 행은 입력에 대한 출력의 편미분이 됩니다.

행렬 사이즈는 [40964096]이 됩니다. 만약 여기서 100개의 미니 배치를 갖고 있다면 [409600409600] size를 갖게 됩니다.
이것은 너무 거대해서 작업에 별로 실용적이지 않습니다.
실제로 행렬을 계산할 필요가 없다는데요. 그렇다면 Jacobian 행렬이 왜 만들어진 것일까요? 각 요소별로 최댓값을 갖는 지점에서 어떤 일이 일어나는지를 생각해본다면 그것은 각각의 편미분한 값과 이어질 것입니다.
입력의 어떤 차원이 출력의 어떤 차원에 영향을 주는지, 그래서 Jacobian 행렬은 대각선 형태의 구조를 볼 수 있습니다. 입력의 각 요소는 오직 출력의 해당 요소에만 영향을 주기 때문에 Jacobian 행렬은 대각 행렬이 될 것입니다.
실제로 공식화할 필요는 없고, 계산한 gradient 값만 채워넣으면 된다고 합니다. Jacobian 행렬은 벡터 미적분학에서 다변수 벡터 함수의 도함수 행렬입니다. 야코비 행렬식(영어: Jacobian determinant)은 야코비 행렬의 행렬식을 뜻합니다.
A vectorized example
이제 세 번째로 vectorized example을 보게 됩니다.

하나의 example입니다.

backward pass를 시작하기 전 1부터 시작합니다.
그리고 $f$에 대한 $q$의 미분을 하면 $2q_i$가 되고, 이는 $\nabla_qf=2q$로도 표현됩니다.

그 다음 미분을 계산합니다. chain rule에 의해 계산되는 것을 볼 수 있습니다.
$Σ(2q_i)(1_k=x_{i,j})$로 계산되고, 마찬가지로 $\nabla_wf=2q*x^T$ 로 나타낼 수 있습니다.
미분 식은 항상 변수와 같은 shape을 갖게 됩니다.

마지막으로 $f$에 대한 $x$의 미분도 위의 과정으로 이루어집니다. 여기까지의 과정이 computational graph에서 실제로 모듈화 된 구현과 같습니다. 각 노드를 local하게 보았고, upstream gradient와 함께 chain rule을 이용해서 local gradient를 계산했습니다.
Neural Networks
이제부터 Neural Networks를 살펴볼 겁니다. $W$가 행렬이고 $x$가 입력 column vector로서 이미지의 모든 픽셀 정보값을 가질 때,
$s=Wx$
의 형태의 공식으로 class score를 계산했습니다. 그래서 위 식은 Linear score function라고 합니다.

CIFAR-10의 경우 $x$는 크기가 [3072x1]인 column vector이고, $W$는 크기가 [10x3072]인 행렬이빈다.
따라서 output score는 크기가 [10x1]인 vector가 되었습니다. 만약 layer가 두 개인 Neural Network라면?
$s=W_2 *max(0,W_1x)$
위의 예로 이어 설명하겠습니다.
$W_1$는, [100x3072]인 행렬로서 이미지를 100-d짜리 중간 단계의 벡터가 됩니다. $max(0,−)$ 함수는 비선형함수로서 $W_1x$의 각 원소에 적용됩니다.
이러한 비선형성을 구현하기 위한 방법은 여러 개 있지만, 이 함수는 흔히 쓰이는 것이고 단순히 모든 0 이하 값을 모두 0으로 바꿔버립니다. 마지막으로 행렬 $W_2$는 크기 [10x100]짜리 행렬입니다.
class score로 쓰일 숫자 10개를 계산합니다. parameter $W_2,W_1$는 gradient로 학습시키고, 그 gradient들은 chain rule( backpropagation)으로 계산하여 구합니다.
$s=W_3max(0,W_2max(0,W_1x))$
는 3-layer Neural Network에 해당됩니다.
Artificial Neural Network


🔗 XOR and Simple Neural Network
🔗 퍼셉트론 - Linear Model, Activation Function
이 부분에 대한 개념은 이전에 정리한 포스팅으로 대체하겠습니다. 강의에서는 activation function으로 sigmoid를 예를 들고 있습니다. 이 부분을 코드로 나타내면 이렇습니다.
class Neuron(object):
# ...
def forward(inputs):
""" assume inputs and weights are 1-D numpy arrays and bias is a number """
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
return firing_rate
강의에서는 인공신경망은 인간의 실제 뉴런과 유사하다고 얘기하는 것을 경계하고 있습니다. 실제로 생물학적 뉴런은 종류도 다양하고 훨씬 더 복잡한 연산을 수행하기 때문입니다.
Synapses도 단순히 하나의 가중치만 갖는 것이 아니기 때문에, ANN을 설명할 때 인간의 실제 뉴런과 비교하는 것을 경계하며 설명하였습니다.
Activation Function
그 다음에 이어지는 부분이 활성화 함수(activation function)입니다.

여기에 있는 activation function의 특성을 간단히 알고 가면 좋을 것 같고, 강의 후반에 다룬다고 합니다. 참고로 현재 가장 많이 사용하는 activation function은 ReLU입니다.
Neural networks: Architectures

왼쪽 그림의 경우, 2-layer Neural Net이라고 합니다. 왜 layer가 3개인데 2-layer라고 할까요?
기본적으로 weight를 갖고 있는 것만 layer라고 합니다. 그러면 input layer 같은 경우는 weight를 갖고 있지 않기 때문에 제외가 됩니다.
그래서 2-layer neural network 또는 1-hidden-layer Neural Network라고 부르는 것입니다. 오른쪽 같은 경우도 마찬가지로, 3-layer neural network 또는 2-hidden-layer Neural Network라고 부르게 됩니다.

그리고 파란색 네모 박스를 살펴보시면, 모든 노드들이 연결되어 있습니다. 이런 경우를 Fully-connected layer라고 부르며 줄여서 FC layer라고 합니다.
Example feed-forward computation of a neural network

layer로 구성하는 이유는 효율적으로 계산을 할 수 있기 때문입니다. 행렬 벡터 연산을 사용해 신경망을 구성하여 이 부분에서 효율적이라 합니다.
위 그림에서 3-layer neural network를 떠올려보면 입력은 [3x1] vector입니다. 첫 번째 hidden layer의 가중치 $W_1$은 [4x3]의 크기이고 모든 노드에 대한 bias는 $b_1$ [4x1] vector에 있습니다.
모든 단일 뉴런에서는 가중치 $W_1$가 있으므로 행렬 벡터 곱셈 np.dot(W1,x)는 모든 layer에 있는 뉴런의 활성화를 계산합니다.
hidden layer의 $W_2$는 [4x4] 행렬을, 마지막 output layer에 대한 $W_3$은 [1x4] 행렬이 됩니다.
이 3-layer 신경망의 forward pass는 activation function과 섞인 3개의 행렬 곱셈이라 볼 수 있습니다. 이렇게 layer를 구성해서 연산의 편의성을 가져옵니다. 하나의 layer는 하나의 연산을 통해 계산해 편의성을 제공합니다.
# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)Summary
- 뉴런을 linear layer와 fully-connected로 재배열
- 이 layer는 모든 것을 계산하는데 효율적인 벡터화 된 코드를 사용하는데 좋은 속성을 갖고 있습니다.
- 신경망이 생물학적 뉴런에서 영감을 갖고 있다는 것을 살펴보았습니다.
다음 시간에는 Convolutional Neural Network에 대해 배우게 됩니다. 이번 강의도 모두 고생 많으셨습니다.
포스팅 중 잘못된 내용이 있다면 댓글로 알려주시면 감사하겠습니다. 감사합니다.
'AI > CS231n' 카테고리의 다른 글
| cs231n 8강 정리 - Visualizing and Understanding (0) | 2022.12.05 |
|---|---|
| cs231n 7강 정리 - Training Neural Networks (0) | 2022.11.13 |
| cs231n 5강 정리 - Convolutional Neural Networks (0) | 2022.08.15 |
| CS231n 3강 정리 - Loss Functions and Optimization (0) | 2022.08.14 |
| CS231n 2강 정리 - Image Classification (0) | 2022.08.13 |
- Total
- Today
- Yesterday
- 리눅스 nano
- 도커 작업
- 파이썬 클래스 계층 구조
- Prompt
- 파이썬 딕셔너리
- 리눅스 나노
- cs231n
- 서버구글드라이브연동
- python
- linux nano
- 도커 컨테이너
- Unsupervised learning
- 딥러닝
- 리눅스 나노 사용
- 리눅스
- CNN
- prompt learning
- docker
- clip
- 도커
- 파이썬 클래스 다형성
- 프롬프트
- 퓨샷러닝
- NLP
- 구글드라이브연동
- 파이썬
- few-shot learning
- support set
- stylegan
- style transfer
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

