티스토리 뷰
핸즈온머신러닝의 챕터 8을 공부하고 정리합니다. 참고한 글은 아래 Reference로 남겨두었습니다.
이번 챕터 8의 주제는 Dimension Reduction입니다. 책의 목차는 아래와 같습니다.
- 8.0 개요
- 8.1 차원의 저주
- 8.2 차원 축소를 위한 접근 방법
- 8.3 PCA
- 8.4 커널 PCA
- 8.5 LLE
- 8.6 다른 차원 축소 기법
책 내용을 그대로 정리하진 않을 것 같고, 중요하다고 생각하는 키워드와 개념만 뽑아서 정리해보도록 하겠습니다.
| Keyword
| Curse of dimensionality, Projection, Manifold, PCA, Kernel PCA, LLE
Curse of dimensionality
차원이란 말은 각 sample을 정의하는 정보들로 생각할 수 있습니다. 즉, 각 sample을 정의하는 정보의 개수가 차원입니다.
데이터는 크면 무조건 좋을까요? 같은 모델을 두고 차원의 크기가 주는 영향을 살펴보겠습니다.
$$y = ax_1 + bx_2 + cx_3 + dx_4 + ex_5$$

$x_1$~$x_5$ 의 5개의 변수의 linear combination으로 결정되는 $Y$ 변수입니다.
학습 데이터 sample은 10개이고, dimension에 따른 validation set에서의 예측 성능은 아래의 그림에 나타나 있습니다.

사용하는 sample이 10개이기 때문에 조금씩 올라가는 dimension을 보면 성능이 조금씩 떨어지는 것을 볼 수 있습니다.
여기선 R squared을 사용했습니다. dimension=10 이 될 땐 R squared = 0.55로 성능이 급격히 떨어집니다. 변수의 개수가 sample 수보다 많아지면 (dimension=11) 학습된 모델은 전혀 새로운 데이터를 설명하지 못하게 됩니다. (R squared = 0)
일반적으로 변수보다 학습 데이터가 적은 경우를 underdetermined 된 문제라고 봅니다. 연립 방정식을 세웠을 때 변수보다 식의 개수가 적을 때 해가 무수히 많은 경우와 같습니다.
이해를 위한 다른 예시도 살펴보겠습니다.

각 n-dimension을 가진 모델이 training data의 수가 늘 때 성능이 어떻게 변하는지를 보여주는 그래프입니다.
거의 대부분의 모델은 training data sample 수가 늘수록 성능이 더 좋아집니다.
특히 분홍색의 500 dimension의 모델은 sample 수가 500부터 성능이 눈에 띄게 좋아지고 있는 것을 볼 수 있습니다.
그리고 해당 그래프는 noise가 없는 데이터 임을 참고 부탁드립니다.
정리하자면 한 sample을 특정 짓기 위해서는 고차원 데이터일수록 모델 학습이 어려워지고, 훨씬 더 많은 양의 정보가 필요합니다.
즉, 차원의 저주(Curse of dimensionality)는 데이터의 feature가 많아서 알고리즘 성능이 저하되는 현상을 일컫습니다.
기계학습의 목표는 데이터를 학습시켜 패턴을 찾고, 패턴을 통해 예측하기 위함입니다. 데이터가 high dimensional spaces를 갖는다면 데이터 간 거리가 멀어져 비슷한 특징을 갖는 패턴과 클러스터를 찾기 어려워집니다.
그리고 KNN(K-Nearest Neighbor) 알고리즘을 생각해보면, 데이터가 고차원이 될 때 데이터 간의 거리가 상당히 멀어지는 것을 생각할 수 있습니다.
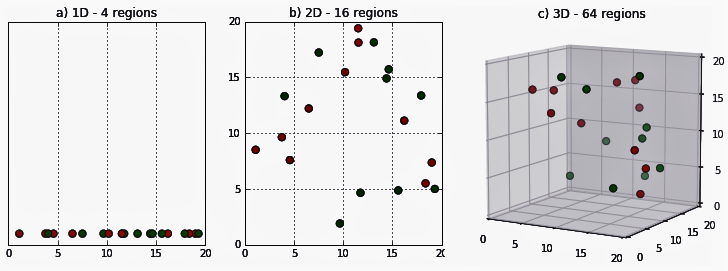
KNN은 가장 특성이 비슷한 data point들끼리 모아 평균으로 예측치를 내는 방법이기 때문에 차원이 커지면 근접한 이웃의 거리가 점점 멀어지며 설명력이 떨어집니다.
그렇다면 해결 방법으로는 1) 고차원 데이터일 수록 더 많은 데이터 양이 필요하다는 것을 알 수 있고, 2) 차원 축소의 방법을 사용해서 feature의 개수를 축소시킬 수 있습니다.
그래서 핸즈온머신러닝의 챕터 8은 curse of dimensionality의 개념을 설명한 다음 차원 축소 기법에 대한 설명으로 넘어갑니다.
Projection
실제 training sample들은 high dimension spaces에 균일하게 퍼져 있는 것이 아닌 그 안의 low dimension subspace에 놓여 있습니다.

3차원 공간에 training sample이 평면 형태로 놓여 있습니다. sample들이 2차원 subspace로 나타난 것입니다.
이렇게 3차원에 있는 sample들을 subspace에 수직으로 투영하여 2차원 dataset을 얻는 방법을 projection이라 합니다.
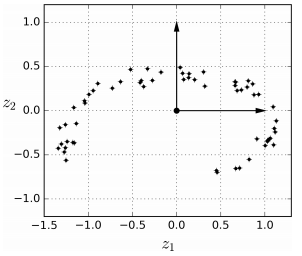
Projection의 개념은 PCA와 이어집니다.
Porjection이 항상 좋은 방법은 아닙니다. 어떤 경우에는 데이터가 swiss roll처럼 생겨 공간이 뒤틀리는 현상이 발생합니다. 이 경우에는 projection하면 구분하기가 더 어려워집니다.
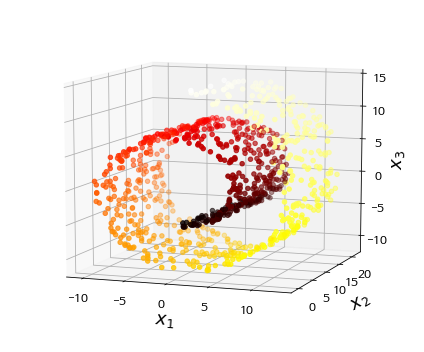
Manifold
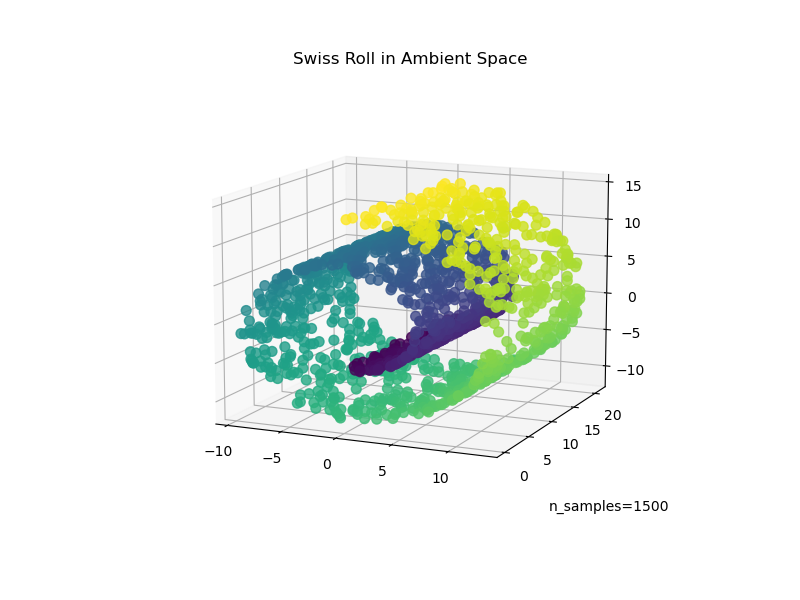
위에서도 봤던 swiss roll은 2D manifold의 한 예시입니다. 2D manifold는 high dimension space에서 뒤틀린 2D 모양입니다. 그리고 d-dim manifold는 n-dim의 일부입니다. (d<n)
많은 dimension reduction algorithms이 training sample이 놓여 있는 manifold를 모델링하는 식으로 작동합니다. 이를 manifold learning이라고 합니다. 대부분 실제 고차원 데이터셋이 더 낮은 저차원 manifold에 가깝게 놓여 있다는 가정에 근거합니다.
또한, manifold는 저차원의 공간에 표현되면 더 간단해질 거란 가정이 따라오지만 꼭 그렇지 않습니다.
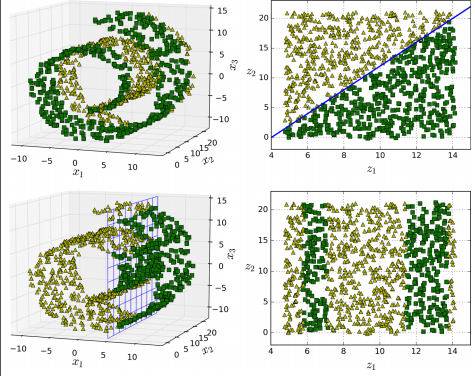
1행의 그래프를 보면 manifold space인 2D에서는 decision boundary가 단순해집니다. 반면, 2행의 그래프는 3D에서의 decision boundary가 수직 평면으로 더 간단히 표현됩니다.
결론적으로는 차원을 감소시키면 훈련 속도는 빨라지지만, 성능이 더 나아지는 것은 아니라는 점입니다. dataset에 따라 다릅니다.
swiss roll은 뒤에 나오는 개념인 LEE와 t-SNE와도 관련이 있습니다.

PCA(Principal Component Analysis)
PCA는 주성분 분석이라고도 말하며, 가장 인기 있는 차원 축소 알고리즘입니다. 데이터에 가장 가까운 hyperplane을 정의한 다음 데이터를 평면에 projection하는 방법입니다.
| PCA
| To find a set orthogonal bases to preserve the variance of the original data
PCA의 main idea는 variance가 최대한 보존되는 축을 선택합니다. 모든 차원이 직교가 되도록 새로운 차원 집합을 찾고 데이터의 분산에 따라 순위가 매겨집니다. 더 중요한 기본 축이 먼저 발생한다는 의미입니다.
PCA 작동 방식
1. 데이터 포인트의 공분산 행렬 $X$를 계산
2. eigen vector와 해당 eigen value를 계산
3. eigen value에 따라 eigen vector를 내림차순으로 정렬
4. 첫 번째 k eigen vector를 선택하면 새로운 k 차원이 됨
5. 원래의 n차원 data point들을 k차원으로 변환
Reference
[1] https://thesciencelife.com/archives/1001
[2] https://modern-manual.tistory.com/4
[3] https://scikit-learn.org/stable/auto_examples/manifold/plot_swissroll.html
[4]
'AI > Machine Learning' 카테고리의 다른 글
| 기초 확률, 가우시안 분포, 커널밀도추정, 최근접 이웃 접근법 (0) | 2023.04.27 |
|---|---|
| 머신러닝 면접 기출 질문과 답변 정리 - Machine Learning Interview Questions and Answers (0) | 2022.05.25 |
| Data Science vs. Machine Learning - 공통점과 차이점 (0) | 2022.05.24 |
| [핸즈온 머신러닝] 챕터 9 비지도 학습 (clustering, k-means, DBSCAN, GMM) (0) | 2022.05.22 |
- Total
- Today
- Yesterday
- 딥러닝
- support set
- stylegan
- 리눅스 나노 사용
- 구글드라이브연동
- 파이썬 클래스 다형성
- 퓨샷러닝
- clip
- Prompt
- 도커
- linux nano
- 도커 작업
- CNN
- style transfer
- python
- docker
- Unsupervised learning
- 파이썬 딕셔너리
- NLP
- cs231n
- 리눅스 nano
- 서버구글드라이브연동
- 파이썬
- few-shot learning
- 파이썬 클래스 계층 구조
- prompt learning
- 리눅스
- 리눅스 나노
- 도커 컨테이너
- 프롬프트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |

