티스토리 뷰
EEG Data Analysis (FFT, SFTF, Filtering, window function, PSD, Spectrogram)
Suyeon Cha 2022. 8. 1. 23:06참고
[1] STFT(Short Time Fourier Transform) - 1편
[2] STFT(Short Time Fourier Transform) 2편
[3] 푸리에 변환과 스펙트럼
1. EEG
- EEG는 뇌파 신호를 의미합니다. (Electroencephalography의 줄임말)
쉽게 설명하면 두피에서 나오는 전기를 기록하는 방법인데요. 뇌의 뉴런 내의 이온 전류로 인한 전압 변동을 측정한다고 합니다. 여러 전극에서 기록된 일정 기간 동안의 뇌의 활동이 기록됩니다.

- EEG엔 5가지 주파수 범위가 있음 (연구에 따라 범위는 다르게 정의될 수 있음)

- channel은 사용된 electrodes의 수이며, 위치에 따라 나뉩니다.


- sampling rate는 초당 sample
- Low-pass filter / High-pass filter
- Low-pass Filter는 낮은(Low) 주파수 영역의 정보만 통과(Pass)시키는 필터
- High-pass Filter는 높은(High) 주파수 영역의 정보만 통과(Pass)시키는 필터
- 두 filter를 결합하여 특정 주파수 영역대만 통과 시키는 Band-pass filter를 만들 수 있음. → 원하는 주파수의 정보만 뽑아서 받아들이기 위해
2. Filtering 하는 이유
- 관심 범위를 초과하거나 미만이 되는 신호를 줄이며 영향을 최소화 → 노이즈 제거
- 특정 임계값을 통해 최소한의 높은 주파수를 차단하고, 이를 low-pass filter라고 함
- 흔히, aliasing으로 알려진 현상은 실제 signal보다 sampling된 주기가 더 낮은 경우에 발생하여 신호를 왜곡하는 현상을 일컫는다. (→ 정보 손실, 정보 왜곡)
- sampling rate는 가장 높은 frequency를 capture할 수 있을만큼 충분히 높아야 하며, Nyquist sampling theorem에 따라 fs≥2fc 이어야 함
- fs: sampling frequency, fc: highest frequency
- 따라서 pre-filter 필요 (quality 향상,noise 제거 등)
3. FIR, IIR filter

- FIR filter (Finite Impulse Response Filter)
- IIR filter (Infinite Impulse Response Filter)
- 각 필터는 impulse의 길이에 따라 분류된다.Figure. FIR vs. IIR
- 스펙트럼 감쇠 정도가 비슷하지만, 위상이 선형인지 비선형인지가 다름
- FIR: 모든 주파수가 동일한 양만큼 시간에 따라 이동하므로 필터링할 신호에 위상 왜곡이 발생하지 않음. 이전 출력값을 사용하지 않아서 어떤 유형의 입력 신호에도 안정적임 / 연산 및 메모리가 많이 필요
- IIR: 선형 위상이 중요하지 않고 메모리가 제한된 애플리케이션에서 사용. 적은 메모리 사용, 계수 수가 적어서 real-time 제어가 가능
4. Window function (Hamming)
- Fourier transform을 적용하도록 도와주는 역할
- 푸리에 변환(Fourier transform)은 시간축의 신호를 주파수 축의 정보로 변환하는 방법
- 디지털 신호가 필요하여 이산 신호를 위한 DFT를 사용하고, DFT는 유한한 sample signal에 대한 변환을 수행하고 연산이 많이 필요함
- DFT를 사용하며 sample 끝 구간에서 오류 정보를 갖게 됨. 이를 해결하기 위해 사용하는 방법이 window function임
- window는 sample 된 구간의 맨 앞쪽과 뒤쪽의 신호가 0으로 변하게 하고, 나머지 구간 모두 0으로 간주하도록 유도함
- Hamming window
- overlap을 같이 수행할 경우 데이터 손실을 줄일 수 있음
- 방식
- data에 convolution하는 방법 (window function을 filter로 쓰는 방법)
- 대부분의 window function은 주파수 축에서 low-pass filter 형태를 띄고 있으므로, 이 방법을 쓰게 되면 신호 자체가 smoothing되는 결과를 가짐
- data에 곱해서 사용하는 방법F{s′(t)}=F{s(t)⋅w(t)}=F{s(t)}∗F{w(t)} 이
- 이는 결국 주파수축에서 filtering 한 것과 같음
- 시간 축에서 곱하는 건 Fourier transform된 주파수 축에서 convolution한 것
5. PSD(Power Spectral Density)
- psd는 signal의 frequency에 따른 power의 밀도를 표현한 것
- random signal을 특성화하는데 사용된다. (실제 signal은 random한 경우가 더 많음)
- Time signal

- 주파수가 시간이 지남에 따라 변하는 신호
- FFT

- 신호의 주파수 성분이 10Hz, 20Hz, 30Hz로 이루어져 있고, 3가지 주파수 성분이 어느 시점에 존재하는지는 알 수 없음. 복잡할수록 알기 어려워지며 이에따라 기본 Time-Frequency 분석 기법인 STFT가 생기게 된 것
- time domain을 frequency domain으로 변환
- sampling rate를 벗어난 경우 이해하기 어려운 결과
- DFT를 더 효율적으로 계산하는데 사용하는 알고리즘. 주파수의 함수로 진동 진폭을 출력하므로 진동이 유발하는 원인을 이해할 수 있음.
- Spectrogram

- 일련의 FFT를 사용하여 spectrum(frequency domain)이 time에 따라 어떻게 변하는지 설명하기 위해 FFT를 겹쳐 사용
- 특정 시점에 대해 확장한 개념이 스펙트로그램. 즉, 시간의 흐름을 가지는 푸리에 변환
- STFT의 단순히 magnitude 부분을 취해서 db스케일로만 변환해주면 spectrogram이 된다.
- x-axis: time / y-axis: frequency spectrum
- STFT

- 시간과 주파수 2개의 축으로 이루어져 있음. 신호에 대해 자신이 알고 싶은 시점에서 주파수 성분을 알 수 있음.
- 결론적으로 STFT는 시간에 따라 특성이 변하는 신호를 분석하는데 사용됨
- STFT는 신호의 구간을 나누는 것
- window는 주파수 정보를 시간에 대한 축으로 표현할 때 사용함
- STFT의 가장 큰 단점은 초기 신호를 Windwo length에 따라서 분리시켜서 푸리에 변환에 사용되는 신호의 길이를 감소시킴
- 따라서 주파수 Resolution이 악화됨
- 그렇다고 Window length를 증가시켜 주파수 Resolution을 향상시켜도 시간에 대한 Resolution은 반대로 악화됨
- 이러한 주파수와 시간의 Trade off 관계로 인한 Resolution의 한계를 완화시키기 위한 방법이 Overlap임
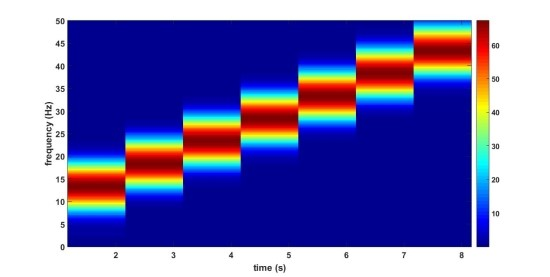
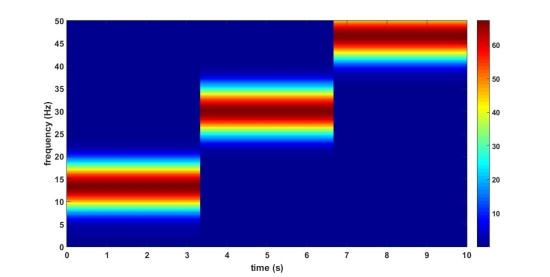
위의 그림을 보면 같은 신호지만 window length에 따라 표현이 달라집니다.
window length가 작을 경우, 그림 1과 같이 시간에 대한 resolution이 좋아집니다. 반대로 커질 경우, 그림 2와 같이 시간 resolution이 단순해집니다.
다음은 Overlap을 적용하겠습니다. overlap이란 wIndow를 적용할 때 window가 서로 겹쳐져 적용되는 것을 말합니다.

overlap을 적용하지 않은 왼쪽과 적용한 오른쪽의 그림입니다.
적용하면 window가 서로 겹쳐지면서 더 많은 window가 적용되고 이에 따라 시간에 따른 resolution이 좋아집니다.

위 그림은 overlap을 70% 정도 적용한 경우입니다.
여기까지 eeg dataset에 대한 설명과 필터링, window function, overlap, Time signal, FFT, SFTF 등을 살펴보았습니다.
'AI' 카테고리의 다른 글
| Online Continual Learning 개념 정리 (0) | 2023.05.16 |
|---|---|
| MNE 파이썬 오픈소스 패키지 소개 (for human neurophysiological data) (0) | 2022.08.01 |
- Total
- Today
- Yesterday
- docker
- 도커 작업
- stylegan
- python
- 파이썬 클래스 계층 구조
- 서버구글드라이브연동
- NLP
- style transfer
- 파이썬 딕셔너리
- Prompt
- few-shot learning
- support set
- 도커 컨테이너
- Unsupervised learning
- CNN
- linux nano
- 파이썬
- 리눅스
- 프롬프트
- clip
- 도커
- 퓨샷러닝
- 파이썬 클래스 다형성
- 딥러닝
- 리눅스 나노 사용
- prompt learning
- 리눅스 나노
- 구글드라이브연동
- 리눅스 nano
- cs231n
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |

